题目内容
(本小题满分12分)已知等差数列{ }的公差
}的公差 ,它的前n项和为
,它的前n项和为 ,若
,若 ,且
,且 成等比数列,
成等比数列,
(Ⅰ)求数列{ }的通项公式;
}的通项公式;
(Ⅱ)若数列{ }的前n项和为
}的前n项和为 ,求证:
,求证: 。
。
(Ⅰ)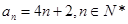 ;(Ⅱ)
;(Ⅱ)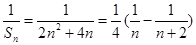 ,
,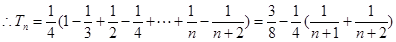 ,显然,
,显然, 。
。
解析试题分析:(Ⅰ)由已知,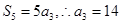 ,
,
又 成等比数列,由
成等比数列,由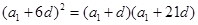 且
且 可解得
可解得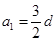 ,
, ,故数列{
,故数列{ }的通项公式为
}的通项公式为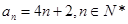 ;
;
(Ⅱ)证明:由(Ⅰ),
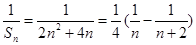 ,
,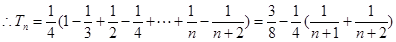
显然, 。
。
考点:等差数列的性质;等比数列的性质;等差数列的通项公式;数列的前n项和的求法。
点评:常见的裂项公式: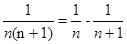 ,
,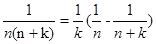 ,
,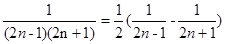 ,
,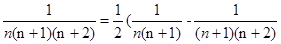 ,
,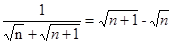 ,
,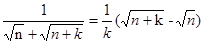 。
。

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
在等差数列{an}中,其前n项和是 ,若
,若 ,则在
,则在 中最大的是( )
中最大的是( )
A. | B. | C. | D. |
已知数列{ }中,
}中, =
= ,
, +
+ (n
(n ,则数列{
,则数列{ }的通项公式为( )
}的通项公式为( )
A. | B. |
C. | D. |
 的前
的前 项和为
项和为 ,
,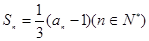
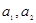 ;
; 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,且对任意的
项和,且对任意的 ,有
,有 .
. ,求数列
,求数列 的前
的前 .
.  是等差数列,
是等差数列, ,数列
,数列 的前n项和是
的前n项和是 ,且
,且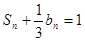 .
. ﹜满足:
﹜满足: .(Ⅰ)求数列﹛
.(Ⅰ)求数列﹛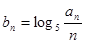 ,求
,求
 an-1+1 (n≥2)
an-1+1 (n≥2) 
