题目内容
若a>b>0,求证:aabb>abba.
答案:
解析:
解析:
|
证明:∵a>b>0, ∴ ∴ 又abba>0,∴aabb>abba. 由于对数可使运算降级,也可取对数后作差比较. 证明:lg(aadb)-lg(abba)=(a lga+b lgb)-(b lga+a lgb) =(a-b)lga+(b-a)lgb =(a-b)(lga-lgb)>0. ∴lg(aabb)>lg(abba), 故aabb>abba. |

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
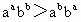 .
.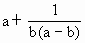 的最小值为3.
的最小值为3.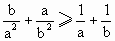 ;
;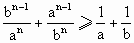 .
.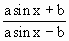 不能介于
不能介于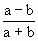 与
与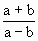 之间.
之间.