题目内容

证明:假设三个式子都大于 ,
,
即(1-x)y > , (1-y)z>
, (1-y)z> , (1-z)x>
, (1-z)x> ,
,
三个式子相乘得:
(1-x)y · (1-y)z·(1-z)x> -------①
-------①
∵0<x<1 ∴x(1-x)≤( )
) =
=
同理:y(1-y)≤ , z(1-z)≤
, z(1-z)≤ ,
,
∴(1-x)y · (1-y)z·(1-z)x≤ ------②
------②
显然①与②矛盾,所以假设是错误的,故原命题成立.----12分
 ,
,即(1-x)y >
 , (1-y)z>
, (1-y)z> , (1-z)x>
, (1-z)x> ,
,三个式子相乘得:
(1-x)y · (1-y)z·(1-z)x>
 -------①
-------①∵0<x<1 ∴x(1-x)≤(
 )
) =
=
同理:y(1-y)≤
 , z(1-z)≤
, z(1-z)≤ ,
,∴(1-x)y · (1-y)z·(1-z)x≤
 ------②
------②显然①与②矛盾,所以假设是错误的,故原命题成立.----12分
本试题主要是考查了反证法证明的运用。先反设,然后在此基础上推理论证,得到一个矛盾,从而说明原命题的正确性。

练习册系列答案
相关题目

 、
、 、
、 、
、 是任意实数
是任意实数 则( )
则( )







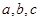 是正实数,则下列说法正确的个数是( )
是正实数,则下列说法正确的个数是( )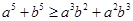
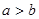 ,则
,则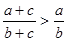
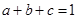 ,则
,则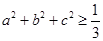
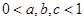 ,则
,则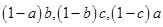 可都大于
可都大于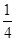




 恒成立,
恒成立,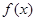 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时, 的解集是_______________.
的解集是_______________. 
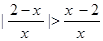 的解是___________
的解是___________ ,则
,则 的大小关系是( )
的大小关系是( )


 的取值确定
的取值确定 、
、 、
、 、
、 都是正数,
都是正数, ,则有( )
,则有( ) <1
<1