题目内容
已知函数f(x)=2sinxcosx-2sin2x+1(x∈R).(Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)若在△ABC中,角A,B,C的对边分别为a,b,c,
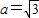 ,A为锐角,且
,A为锐角,且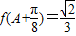 ,求△ABC面积S的最大值.
,求△ABC面积S的最大值.
【答案】分析:(Ⅰ)利用同角三角函数基本关系将f(x)=2sinxcosx-2sin2x+1(x∈R)转化为f(x)=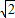 sin(2x+
sin(2x+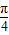 ),利用正弦函数的性质即可求函数f(x)的最小正周期和单调递增区间;
),利用正弦函数的性质即可求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)由f(A+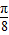 )=
)=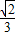 ,可求得cos2A=
,可求得cos2A= ,而A为锐角,可求得cosA、sinA,又a=
,而A为锐角,可求得cosA、sinA,又a=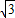 ,利用余弦定理与基本不等式可得bc≤
,利用余弦定理与基本不等式可得bc≤ +
+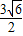 ,从而可求得△ABC面积S的最大值.
,从而可求得△ABC面积S的最大值.
解答:解:(Ⅰ)∵f(x)=2sinxcosx-sin2x+1
=2sinxcosx+cos2x
=sin2x+cos2x
=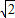 (
(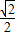 sin2x+
sin2x+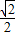 cos2x)
cos2x)
=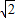 sin(2x+
sin(2x+ )---(2分)
)---(2分)
∴f(x)的最小正周期为π;--------------------(3分)
∵-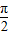 +2kπ≤2x+
+2kπ≤2x+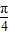 ≤
≤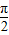 +2kπ(k∈Z),
+2kπ(k∈Z),
∴-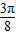 +kπ≤x≤
+kπ≤x≤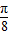 +kπ(k∈Z),
+kπ(k∈Z),
∴f(x)的增区间为(-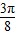 +kπ,
+kπ,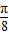 +kπ)(k∈Z),-----------(6分)
+kπ)(k∈Z),-----------(6分)
(Ⅱ)∵f(A+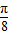 )=
)=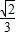 ,
,
∴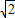 sin(2A+
sin(2A+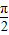 )=
)=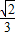 ,
,
∴cos2A= ,
,
∴2cos2A-1= ,
,
∵A为锐角,即0<A<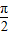 ,
,
∴cosA=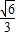 ,
,
∴sinA=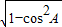 =
=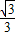 .--------------------(8分)
.--------------------(8分)
又∵a= ,由余弦定理得:a2=b2+c2-2bccosA,即
,由余弦定理得:a2=b2+c2-2bccosA,即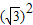 =b2+c2-2bc•
=b2+c2-2bc•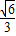 ,
,
∵b2+c2≥2bc,
∴bc≤ +
+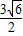 .-------------------------(10分)
.-------------------------(10分)
∴S= bcsinA≤
bcsinA≤ (
( +
+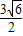 )•
)•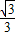 =
=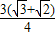 .---------(12分)
.---------(12分)
点评:本题考查同角三角函数基本关系,考查正弦函数的单调性与最值,突出余弦定理与基本不等式的应用,综合性强,属于中档题.
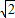 sin(2x+
sin(2x+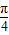 ),利用正弦函数的性质即可求函数f(x)的最小正周期和单调递增区间;
),利用正弦函数的性质即可求函数f(x)的最小正周期和单调递增区间;(Ⅱ)由f(A+
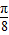 )=
)=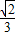 ,可求得cos2A=
,可求得cos2A= ,而A为锐角,可求得cosA、sinA,又a=
,而A为锐角,可求得cosA、sinA,又a=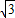 ,利用余弦定理与基本不等式可得bc≤
,利用余弦定理与基本不等式可得bc≤ +
+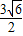 ,从而可求得△ABC面积S的最大值.
,从而可求得△ABC面积S的最大值.解答:解:(Ⅰ)∵f(x)=2sinxcosx-sin2x+1
=2sinxcosx+cos2x
=sin2x+cos2x
=
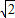 (
(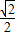 sin2x+
sin2x+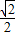 cos2x)
cos2x)=
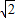 sin(2x+
sin(2x+ )---(2分)
)---(2分)∴f(x)的最小正周期为π;--------------------(3分)
∵-
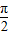 +2kπ≤2x+
+2kπ≤2x+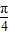 ≤
≤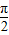 +2kπ(k∈Z),
+2kπ(k∈Z),∴-
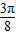 +kπ≤x≤
+kπ≤x≤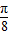 +kπ(k∈Z),
+kπ(k∈Z),∴f(x)的增区间为(-
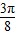 +kπ,
+kπ,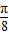 +kπ)(k∈Z),-----------(6分)
+kπ)(k∈Z),-----------(6分)(Ⅱ)∵f(A+
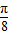 )=
)=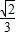 ,
,∴
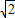 sin(2A+
sin(2A+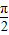 )=
)=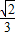 ,
,∴cos2A=
 ,
,∴2cos2A-1=
 ,
,∵A为锐角,即0<A<
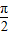 ,
,∴cosA=
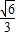 ,
,∴sinA=
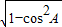 =
=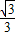 .--------------------(8分)
.--------------------(8分)又∵a=
 ,由余弦定理得:a2=b2+c2-2bccosA,即
,由余弦定理得:a2=b2+c2-2bccosA,即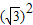 =b2+c2-2bc•
=b2+c2-2bc•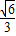 ,
,∵b2+c2≥2bc,
∴bc≤
 +
+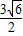 .-------------------------(10分)
.-------------------------(10分)∴S=
 bcsinA≤
bcsinA≤ (
( +
+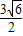 )•
)•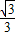 =
=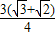 .---------(12分)
.---------(12分)点评:本题考查同角三角函数基本关系,考查正弦函数的单调性与最值,突出余弦定理与基本不等式的应用,综合性强,属于中档题.

练习册系列答案
相关题目