题目内容
已知![]() ,函数
,函数![]() .
.
当![]() 时,求所有使
时,求所有使![]() 成立的
成立的![]() 的值;
的值;
(2)当![]() 时,求函数
时,求函数![]() 在闭区间
在闭区间![]() 上的最小值;
上的最小值;
(3)试讨论函数![]() 的图像与直线
的图像与直线![]() 的交点个数
的交点个数
(1)(2)
(3)
当![]() 时,有1个交点;
时,有1个交点;
当![]() 时,有2个交点;
时,有2个交点;
当![]() 时有3个交点;
时有3个交点;
当![]() 时,有2个交点;
时,有2个交点;
当![]() 时,有3个交点.
时,有3个交点.
解析:
(1)![]() 所以
所以![]() 或
或![]() ;
;
(2)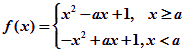 ,
,
1O.当![]() 时,
时,![]() ,这时,
,这时,![]() 对称轴
对称轴![]() ,
,
所以函数![]() 在区间
在区间![]() 上递增,
上递增,![]() ;
;
2O.当![]() 时,
时,![]() 时函数
时函数![]() ;
;
3O.当![]() 时,
时,![]() ,这时,
,这时,![]() 对称轴
对称轴![]() ,
,
![]()
![]() 所以函数
所以函数![]() ;
;
(3)因为![]() 所以
所以![]() ,所以
,所以![]() 在
在![]() 上递增;
上递增;
![]() 在
在![]() 递增,在
递增,在![]() 上递减.
上递减.
因为![]() ,所以当
,所以当![]() 时,函数
时,函数![]() 的图像与直线
的图像与直线![]() 有2个交点;
有2个交点;
又![]() 当且仅当
当且仅当![]() 时,等号成立.
时,等号成立.
所以,当![]() 时,函数
时,函数![]() 的图像与直线
的图像与直线![]() 有1个交点;
有1个交点;
当![]() 时,函数
时,函数![]() 的图像与直线
的图像与直线![]() 有2个交点;
有2个交点;
当![]() 时,函数
时,函数![]() 的图像与直线
的图像与直线![]() 有3个交点;
有3个交点;
当![]() 时,函数
时,函数![]() 的图像与直线
的图像与直线![]() 有2个交点;
有2个交点;
当![]() 时,函数
时,函数![]() 的图像与直线
的图像与直线![]() 有3个交点.
有3个交点.

练习册系列答案
相关题目
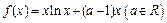 .
. 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;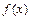 在区间
在区间 上的最小值;
上的最小值;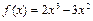 在区间
在区间 内有两个不相等的实数根,求实数a的取值范围.
内有两个不相等的实数根,求实数a的取值范围. 当
当 时,求曲线
时,求曲线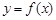 在点
在点 处的切线方程;求函数
处的切线方程;求函数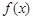 的极值
的极值 当
当 时,求不等式
时,求不等式 的解集;若
的解集;若 的解集包含
的解集包含 ,求a的取值范围。
,求a的取值范围。