题目内容
已知函数![]()
当![]() 时,求该函数的定义域和值域;
时,求该函数的定义域和值域;
如果![]() 在区间
在区间![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
(1)定义域为![]() ;值域为
;值域为![]() (2)
(2)![]()
解析:
(1) 当![]() 时,
时,![]()
令![]() ,解得
,解得![]()
所以函数![]() 的定义域为
的定义域为![]() .
.
令![]() ,则
,则![]()
所以![]()
因此函数![]() 的值域为
的值域为![]()
(2) 解法一:![]() 在区间
在区间![]() 上恒成立等价于
上恒成立等价于![]() 在区间
在区间![]() 上恒成立
上恒成立
令![]()
当![]() 时,
时,![]() ,所以
,所以![]() 满足题意.
满足题意.
当![]() 时,
时,![]() 是二次函数,对称轴为
是二次函数,对称轴为![]() ,
,
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是增函数,
上是增函数,![]() ,所以
,所以![]() 满足题意;
满足题意;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是减函数,
上是减函数,![]() ,
,
解得![]() ,所以
,所以![]() 满足题意.
满足题意.
综上,![]() 的取值范围是
的取值范围是![]()
解法二:![]() 在区间
在区间![]() 上恒成立等价于
上恒成立等价于![]() 在区间
在区间![]() 上恒成立
上恒成立
由![]() 且
且![]() 时,
时,![]() ,得
,得![]()
因为![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
 已知函数
已知函数 的图象经过点(4,8).
的图象经过点(4,8).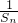 成等差数列,并求数列{an}的通项公式;
成等差数列,并求数列{an}的通项公式; 时,求上表中第k(k≥3)行所有项的和.
时,求上表中第k(k≥3)行所有项的和. (
( ,c是实数常数)的图像上的一个最高点
,c是实数常数)的图像上的一个最高点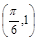 ,与该最高点最近的一个最低点是
,与该最高点最近的一个最低点是 ,
, 的解析式及其单调增区间;
的解析式及其单调增区间;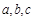 ,且
,且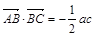 ,角A的取值范围是区间M,当
,角A的取值范围是区间M,当 时,试求函数
时,试求函数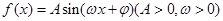 的部分
的部分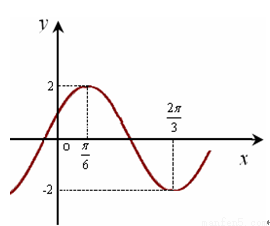
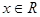 时,求该函数图象的对称轴方程和对称中心坐标;(4分)
时,求该函数图象的对称轴方程和对称中心坐标;(4分) 的单调增区间;(3分)
的单调增区间;(3分)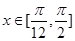 ,求
,求 ,且该函数图像的对称中心到对称轴的最小距离为
,且该函数图像的对称中心到对称轴的最小距离为 当
当 时,f(x)的最大值为1。
时,f(x)的最大值为1。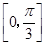 上恒成立,求m的范围.
上恒成立,求m的范围.