题目内容
6.已知|${\overrightarrow a}$|=|${\overrightarrow b}$|,且|${\overrightarrow a$+$\overrightarrow b}$|=$\sqrt{3}$|${\overrightarrow a$-$\overrightarrow b}$|,则向量$\overrightarrow a$与$\overrightarrow b$的夹角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
分析 可以看出,需对等式$|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{3}|\overrightarrow{a}-\overrightarrow{b}|$两边平方,再带入$|\overrightarrow{a}|=|\overrightarrow{b}|$,便可得到${\overrightarrow{b}}^{2}+2{\overrightarrow{b}}^{2}cos<\overrightarrow{a},\overrightarrow{b}>+{\overrightarrow{b}}^{2}$=$3{\overrightarrow{b}}^{2}-6{\overrightarrow{b}}^{2}cos<\overrightarrow{a},\overrightarrow{b}>+3{\overrightarrow{b}}^{2}$,这样显然可以求出$cos<\overrightarrow{a},\overrightarrow{b}>$,从而便可得出$\overrightarrow{a}$与$\overrightarrow{b}$的夹角.
解答 解:对$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{3}|\overrightarrow{a}-\overrightarrow{b}|$两边平方得:$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}=3|\overrightarrow{a}-\overrightarrow{b}{|}^{2}$;
∴${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}=3{\overrightarrow{a}}^{2}-6\overrightarrow{a}•\overrightarrow{b}$$+3{\overrightarrow{b}}^{2}$;
∵$|\overrightarrow{a}|=|\overrightarrow{b}|$;
∴${\overrightarrow{b}}^{2}+2{\overrightarrow{b}}^{2}cos<\overrightarrow{a},\overrightarrow{b}>+{\overrightarrow{b}}^{2}$=$3{\overrightarrow{b}}^{2}-6{\overrightarrow{b}}^{2}cos<\overrightarrow{a},\overrightarrow{b}>+3{\overrightarrow{b}}^{2}$;
∴$8cos<\overrightarrow{a},\overrightarrow{b}>=4$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{1}{2}$;
∴$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°.
故选:C.
点评 考查向量数量积的运算及其计算公式,向量夹角的概念及其范围,已知三角函数值求角.

| A. | 3+ln2 | B. | 3-ln2 | C. | $\frac{3}{2}$+ln2 | D. | $\frac{3}{2}$-ln2 |
| A. | 变量X与变量Y有关系的概率为2.5% | |
| B. | 变量X与变量Y没有关系的概率为97.5% | |
| C. | 变量X与变量Y有关系的概率为97.5% | |
| D. | 变量X与变量Y没有关系的概率为99% |
| A. | π | B. | -1 | C. | 1 | D. | $\frac{π}{2}$ |
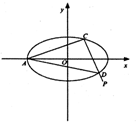 如图,在平面直角坐标系xOy中,A是椭圆G:$\frac{{x}^{2}}{4}$+y2=1的左顶点,过点P(2,-1)任意作一条直线l与椭圆G交于C,D,记直线AC,AD的斜率分别为k1,k2,则$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$的值为-4.
如图,在平面直角坐标系xOy中,A是椭圆G:$\frac{{x}^{2}}{4}$+y2=1的左顶点,过点P(2,-1)任意作一条直线l与椭圆G交于C,D,记直线AC,AD的斜率分别为k1,k2,则$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$的值为-4.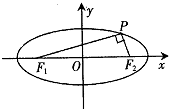 如图,P是椭圆$\frac{{x}^{2}}{4}$+y2=1上的一点,F1,F2是椭圆的两个焦点,且∠F1PF2=90°,则|PF1|•|PF2|等于( )
如图,P是椭圆$\frac{{x}^{2}}{4}$+y2=1上的一点,F1,F2是椭圆的两个焦点,且∠F1PF2=90°,则|PF1|•|PF2|等于( )