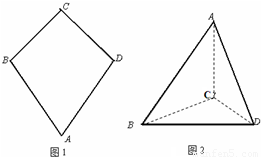
题目内容
如图1,平面四边形ABCD中,A=
C=
,CB=CD=2,且AB=AD.把△ABD沿BD折起(如图2),使二面角A-BD-C的余弦值等于
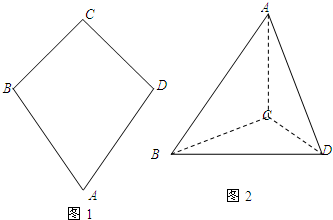
对于图二,完成以下各小题:
(1)求AC的长;
(2)证明:AC⊥平面BCD;
(3)求直线AC与平面ABD所成角的正弦值.
| π |
| 3 |
| π |
| 2 |
| ||
| 3 |
(1)求AC的长;
(2)证明:AC⊥平面BCD;
(3)求直线AC与平面ABD所成角的正弦值.

分析:(1)取BD的中点E,连接AE,CE,由AB=AD,CB=CD,得:AE⊥BD,CE⊥BD,故∠AEC就是二面角A-BD-C的平面角,由此能求出AC.
(2)由AB=AD=BD=2
,得AC=BC=CD=2,AC2+BC2=AB2,AC2+CD2=AD2,故∠ACB=∠ACD=90°,由此能够证明AC⊥平面BCD.
(3)法一:由BD⊥平面ACE,BD?平面ABD,知平面ACE⊥平面ABD,由∠CAF就是AC与平面ABD所成的角,能求出直线AC与平面ABD所成角的正弦值.
法二:设点C到平面ABD的距离为h,由VC-ABD=VA-BCD,解得h=
,由此能求出直线AC与平面ABD所成角的正弦值.
(2)由AB=AD=BD=2
| 2 |
(3)法一:由BD⊥平面ACE,BD?平面ABD,知平面ACE⊥平面ABD,由∠CAF就是AC与平面ABD所成的角,能求出直线AC与平面ABD所成角的正弦值.
法二:设点C到平面ABD的距离为h,由VC-ABD=VA-BCD,解得h=
2
| ||
| 3 |
解答:解:(1)取BD的中点E,连接AE,CE,
由AB=AD,CB=CD,
得:AE⊥BD,CE⊥BD,
∴∠AEC就是二面角A-BD-C的平面角,
∴cos∠AEC=
.
在△ACE中,AE=
,CE=
,
AC2=AE2+CE2-2AE•CE•cos∠AEC
=6+2-2×
×
×
=4,
∴AC=2.
(2)由AB=AD=BD=2
,
得AC=BC=CD=2,AC2+BC2=AB2,AC2+CD2=AD2,
∴∠ACB=∠ACD=90°,
∴AC⊥BC,AC⊥CD,又BC∩CD=C,
∴AC⊥平面BCD.
(3)方法一:由(2)知BD⊥平面ACE,
BD?平面ABD,
∴平面ACE⊥平面ABD,
平面ACE∩平面ABD=AE,作CF⊥AE,交AE于F,
则CF⊥平面ABD,
∠CAF就是AC与平面ABD所成的角,
∴sin∠CAF=sin∠CAE=
=
.
方法二:设点C到平面ABD的距离为h,
∵VC-ABD=VA-BCD,
∴
×
×2
×2
sin60°•h=
×
×2×2×2,
∴h=
,
于是AC与平面ABD所成角θ的正弦为sinθ=
=
.
由AB=AD,CB=CD,
得:AE⊥BD,CE⊥BD,
∴∠AEC就是二面角A-BD-C的平面角,
∴cos∠AEC=
| ||
| 3 |
在△ACE中,AE=
| 6 |
| 2 |
AC2=AE2+CE2-2AE•CE•cos∠AEC
=6+2-2×
| 6 |
| 2 |
| ||
| 3 |
∴AC=2.
(2)由AB=AD=BD=2
| 2 |
得AC=BC=CD=2,AC2+BC2=AB2,AC2+CD2=AD2,
∴∠ACB=∠ACD=90°,
∴AC⊥BC,AC⊥CD,又BC∩CD=C,
∴AC⊥平面BCD.
(3)方法一:由(2)知BD⊥平面ACE,
BD?平面ABD,
∴平面ACE⊥平面ABD,
平面ACE∩平面ABD=AE,作CF⊥AE,交AE于F,
则CF⊥平面ABD,
∠CAF就是AC与平面ABD所成的角,
∴sin∠CAF=sin∠CAE=
| CE |
| AE |
| ||
| 3 |
方法二:设点C到平面ABD的距离为h,
∵VC-ABD=VA-BCD,
∴
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
∴h=
2
| ||
| 3 |
于是AC与平面ABD所成角θ的正弦为sinθ=
| h |
| AC |
| ||
| 3 |
点评:本题考查直线与平面垂直的证明,考查直线与平面所成角的余弦值的求法.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
 如图1,平面四边形ABCD关于直线AC对称,∠A=60°,∠C=90°,CD=2.把△ABD沿BD折起(如图2),使二面角A-BD-C的余弦值等于
如图1,平面四边形ABCD关于直线AC对称,∠A=60°,∠C=90°,CD=2.把△ABD沿BD折起(如图2),使二面角A-BD-C的余弦值等于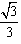 ,对于图2,完成以下各小题:
,对于图2,完成以下各小题:
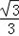 .对于图2,完成以下各小题:
.对于图2,完成以下各小题: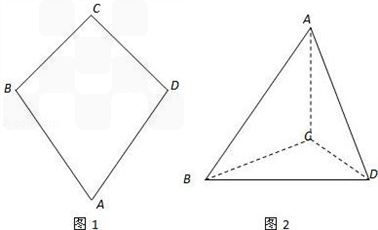
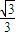 .对于图2:
.对于图2: