题目内容
已知函数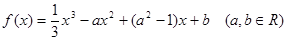 .
.
(Ⅰ)若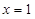 为
为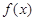 的极值点,求
的极值点,求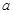 的值;
的值;
(Ⅱ)若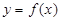 的图象在点(
的图象在点(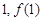 )处的切线方程为
)处的切线方程为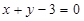 ,求
,求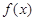 在区间
在区间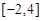 上的最大值;
上的最大值;
(Ⅲ)当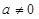 时,若
时,若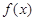 在区间
在区间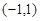 上不单调,求
上不单调,求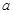 的取值范围.
的取值范围.
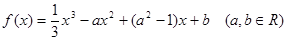 .
.(Ⅰ)若
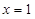 为
为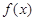 的极值点,求
的极值点,求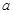 的值;
的值;(Ⅱ)若
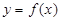 的图象在点(
的图象在点(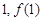 )处的切线方程为
)处的切线方程为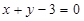 ,求
,求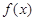 在区间
在区间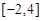 上的最大值;
上的最大值;(Ⅲ)当
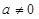 时,若
时,若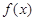 在区间
在区间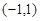 上不单调,求
上不单调,求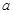 的取值范围.
的取值范围.解:(Ⅰ)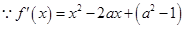 1分
1分
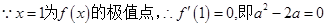
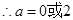 4分
4分
(Ⅱ)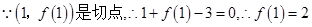
即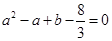
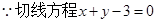 的斜率为-1,
的斜率为-1,
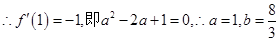 6分
6分
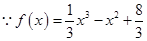
∴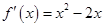 ,可知
,可知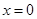 和
和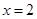 是
是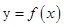 的两个极值点.
的两个极值点.
∵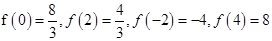
∴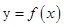 在区间
在区间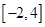 上的最大值为8. 8分
上的最大值为8. 8分
(3)因为函数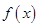 在区间
在区间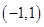 不单调,所以函数
不单调,所以函数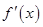 在
在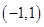 上存在零点,而
上存在零点,而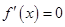 的两根为
的两根为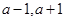 ,区间长为2
,区间长为2
在区间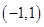 上不可能有两个零点,所以
上不可能有两个零点,所以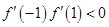 10分
10分
即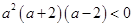 ,
,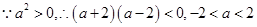
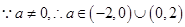 。 12分
。 12分
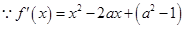 1分
1分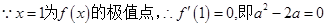
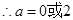 4分
4分(Ⅱ)
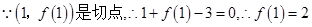
即
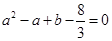
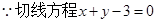 的斜率为-1,
的斜率为-1,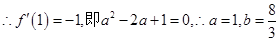 6分
6分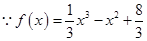
∴
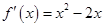 ,可知
,可知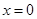 和
和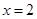 是
是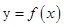 的两个极值点.
的两个极值点.∵
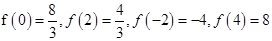
∴
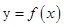 在区间
在区间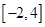 上的最大值为8. 8分
上的最大值为8. 8分(3)因为函数
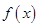 在区间
在区间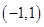 不单调,所以函数
不单调,所以函数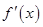 在
在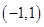 上存在零点,而
上存在零点,而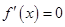 的两根为
的两根为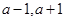 ,区间长为2
,区间长为2在区间
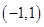 上不可能有两个零点,所以
上不可能有两个零点,所以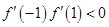 10分
10分即
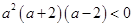 ,
,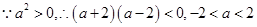
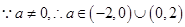 。 12分
。 12分略

练习册系列答案
相关题目
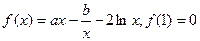 .
.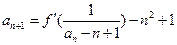 ,已
,已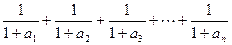 与
与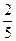 的大小,并说明你的理由.
的大小,并说明你的理由.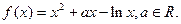
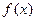 在
在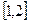 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;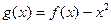 ,是否存在实数
,是否存在实数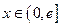 (
(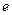 是自然常数)时,函数
是自然常数)时,函数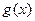
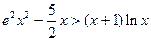 .
.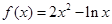 的递增区间是( ).
的递增区间是( ).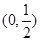
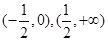
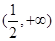
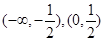
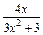 ,x∈[0,2].
,x∈[0,2].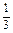 ax3-a2x,x∈[0,2].若对任意x1∈[0,2],总存在x2∈[0,2],使f(x1)-g(x2)=0.求实数a的取值范围.
ax3-a2x,x∈[0,2].若对任意x1∈[0,2],总存在x2∈[0,2],使f(x1)-g(x2)=0.求实数a的取值范围.
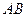 是半圆的直径,点
是半圆的直径,点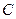 在半圆上,
在半圆上,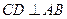 ,垂足为
,垂足为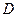 ,且
,且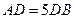 ,设
,设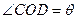 ,则
,则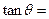
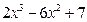 单调递增区间为_______________________。
单调递增区间为_______________________。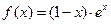 的单调递增区间是 .
的单调递增区间是 .