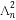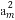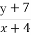设等差数列{an},{bn}的前n项和分别为Sn,Tn,若对任意自然数n都有=,则+的值为 . 题目和参考答案——青夏教育精英家教网—

题目内容

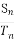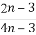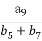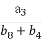设等差数列{an},{bn}的前n项和分别为Sn,Tn,若对任意自然数n都有=,则+的值为　　　.

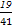
【解析】∵{an},{bn}为等差数列,

∴+=+===.

∵====,∴=.

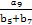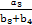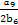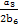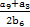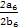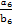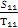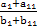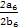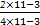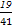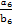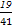【方法技巧】巧解等差数列前n项和的比值问题

关于等差数列前n项和的比值问题,一般可采用前n项和与中间项的关系,尤其是项数为奇数时Sn=na中,也可利用首项与公差的关系求解.另外,熟记以下结论对解题会有很大帮助:若数列{an}与{bn}都是等差数列,且前n项和分别是Sn与Tn,则=.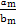

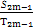练习册系列答案

名校课堂系列答案

相关题目

定义:若数列{An}满足An+1=,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.

(1)证明:数列{2an+1}是 “平方递推数列”,且数列{lg(2an+1)}为等比数列.

(2)设(1)中“平方递推数列”的前n项之积为Tn,即Tn=(2a1+1)(2a2+1)…(2an+1),求数列{an}的通项公式及Tn关于n的表达式.

等差数列{an}的前n项和为Sn,已知am-1+am+1-=0,S2m-1=38,则m=(　　)

(A)38(B)20(C)10(D)9

已知x,y满足条件则的取值范围是(　　)

(A)[,9] (B)(-∞,)∪(9,+∞)

(C)(0,9) (D)[-9,-]

等差数列{an}的各项均为正数,其前n项和为Sn,满足2S2=a2(a2+1),且a1=1.

(1)求数列{an}的通项公式.

(2)设bn=,求数列{bn}的最小值项.

等差数列{an}的前n项和为Sn,若a3+a17=10,则S19=(　　)

(A)55(B)95(C)100(D)不能确定

根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:

对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组,得到频率分布直方图如图.

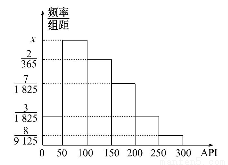
(1)求直方图中x的值.

(2)计算一年中空气质量分别为良和轻微污染的天数.

(3)求该城市某一周至少有2天的空气质量为良或轻微污染的概率.

(结果用分数表示.

已知57=78125,27=128,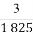++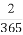++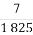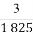=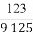,365=73×5).

已知在一个2×2矩阵M的变换作用下,点A(1,2)变成了点A'(4,5),点B(3,-1)变成了点B'(5,1).

(1)求2×2矩阵M.

(2)若在2×2矩阵M的变换作用下,点C(x,0)变成了点C'(4,y),求x,y.

设一次试验成功的概率为p,进行100次独立重复试验,当p=_______时,成功次数的标准差的值最大,其最大值为　　　.

试题分类