题目内容
函数f(x)=ax的反函数为y=f-1(x),若y=f(x+1)的图象过点(3,1),则y=f-1(x+1)的图象经过点( )
分析:根据原函数与反函数图象之间的关系可得结论,对于原函数与复合函数的所过定点问题,本题可利用y=f(x+1)的图象过点(3,1),得到函数f-1(x)的图象一定经过点(1,4),进一步得出y=f-1(x+1)的图象经过点(0,4).
解答:解:由函数y=f(x+1)的图象经过点(3,1),得f(4)=1,则f-1(1)=4,
∴函数f-1(x)的图象一定经过点(1,4)
所以当x=0时有f-1(x+1)=f-1(1)=4,
从而y=f-1(x+1)的图象经过点(0,4).
故选D.
∴函数f-1(x)的图象一定经过点(1,4)
所以当x=0时有f-1(x+1)=f-1(1)=4,
从而y=f-1(x+1)的图象经过点(0,4).
故选D.
点评:本题主要考查复合函数与原函数关系,以及函数与反函数关系,属于基础题.

练习册系列答案
相关题目
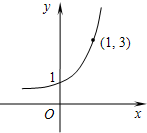 (2007•闵行区一模)(文)已知函数f(x)=ax的图象过点P(1,3),解不等式log3(3-x)-logax<0.
(2007•闵行区一模)(文)已知函数f(x)=ax的图象过点P(1,3),解不等式log3(3-x)-logax<0.