题目内容
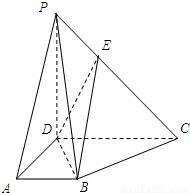
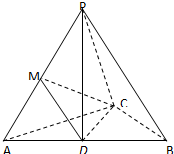 如图,PD⊥平面ABC,AC=BC,D,M分别为AB,PA的中点.求证:
如图,PD⊥平面ABC,AC=BC,D,M分别为AB,PA的中点.求证:(1)PB∥面CDM;
(2)AB⊥PC.
分析:(1)根据DM是△PAB的中位线得到PB∥DM,再利用线面平行判定定理即可证出PB∥面CDM;
(2)由等腰三角形的“三线合一”证出CD⊥AB,结合PD⊥AB利用线面垂直判定定理,证出AB⊥面PCD,从而证出AB⊥PC.
(2)由等腰三角形的“三线合一”证出CD⊥AB,结合PD⊥AB利用线面垂直判定定理,证出AB⊥面PCD,从而证出AB⊥PC.
解答:解:(1)∵△PAB中,D、M分别为AB、PA的中点,
∴DM是△PAB的中位线,可得PB∥DM,…(4分)
∵DM?面CDM,PB?面CDM,
∴PB∥面CDM.…(6分)
(2)∵PD⊥平面ABC,AB?平面ABC,∴PD⊥AB,
又∵AC=BC,D为AB中点,∴CD⊥AB
∵PD、CD是平面PCD内的相交直线
∴AB⊥面PCD,
又∵PC?面PCD,∴AB⊥PC.…(12分)
∴DM是△PAB的中位线,可得PB∥DM,…(4分)
∵DM?面CDM,PB?面CDM,
∴PB∥面CDM.…(6分)
(2)∵PD⊥平面ABC,AB?平面ABC,∴PD⊥AB,
又∵AC=BC,D为AB中点,∴CD⊥AB
∵PD、CD是平面PCD内的相交直线
∴AB⊥面PCD,
又∵PC?面PCD,∴AB⊥PC.…(12分)
点评:本题在三棱锥中证明线面平行和异面垂直,着重考查了线面平行判定定理、线面垂直的判定与性质等知识,属于中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
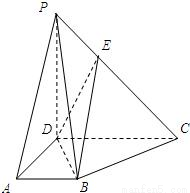
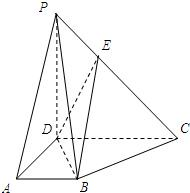 如图:PD⊥平面ABCD,四边形ABCD为直角梯形,AB∥CD,∠ADC=90°,PD=CD=2AD=2AB=2,EC=2PE.
如图:PD⊥平面ABCD,四边形ABCD为直角梯形,AB∥CD,∠ADC=90°,PD=CD=2AD=2AB=2,EC=2PE.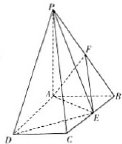 如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F中PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F中PB的中点,点E在边BC上移动.