题目内容
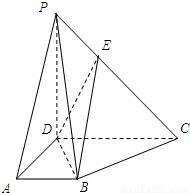
如图:PD⊥平面ABCD,四边形ABCD为直角梯形,AB∥CD,∠ADC=90°,PD=CD=2AD=2AB=2,EC=2PE.(Ⅰ)求证:PA∥平面BDE;
(Ⅱ)求证:平面BDP⊥平面PBC;
(Ⅲ)求二面角B-PC-D的余弦值.
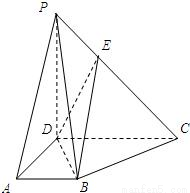
【答案】分析:(1)要证明线面平行,关键是在平面内找到一条可能与已知直线平行的直线,观察到平面BDE中三条已知直线与AE都不平行,故我们要考虑在平面BDE中做一条与PA可能平行直线辅助线,然后再进行证明.
(2)要证明平面BDP⊥平面PBC,我们关键是在一个平面内找到一条与另一个平面垂直的直线,观察图形,在平面PBC中,BC可能与平面BDP垂直,故可以其为切入点进行证明.
(3)要求二面角的余弦,要先构造出二面角的平面角,然后利用解三角形的方法,求出这个平面角的余弦值,进而给出二面角的余弦值.
我们也可以构造空间直角坐标系,求出各点的坐标,进行求出相应直线的方向向量和平面的法向量,利用向量法进行求解.
解答: 解法一:
解法一:
证明:建立如图所示的坐标系,
(Ⅰ)A(1,0,0),B(1,1,0),C(0,2,0),D(0,0,0),P(0,0,2)

 ,
, ,
,
设 ,
,
可得
因为PA?平面BDE,
所以PA∥平面BDE
(Ⅱ)因为
所以 BC⊥BD
BC⊥BD
因为PD⊥平面ABCD,所以BC⊥PD
所以BC⊥平面PBD,
所以平面BDP⊥平面PBC.
(Ⅲ)因为AD⊥DC,AD⊥PD
所以 是平面PDC的法向量,
是平面PDC的法向量, ,设平面PBC的法向量为
,设平面PBC的法向量为 ,
,
由 得:
得: ,
,
设二面角B-PC-D为θ,则cosθ=
所以二面角B-PC-D余弦值为 .
.
解法二:
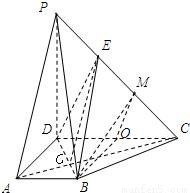 (Ⅰ)连接AC交BD于G,连接EG,
(Ⅰ)连接AC交BD于G,连接EG,
∵AB∥CD
∴ ,由已知
,由已知 ,
,
得 ,
,
∴PA∥EG,
∵EG?平面DEG,PA∉平面DEG
∴PA∥平面DEG.
(Ⅱ)由已知可得, ,取CD的中点O,连接BO,ABOD为正方形,
,取CD的中点O,连接BO,ABOD为正方形,
 ,所以BD2+BC2=CD2由勾股定理的逆定理知BC⊥BD,
,所以BD2+BC2=CD2由勾股定理的逆定理知BC⊥BD,
因为BC⊥PD,所以BC⊥平面BDP,所以平面BDP⊥平面PBC
(Ⅲ)BO⊥CD,BO⊥PD,所以BO⊥平面PDC,BO⊥PC
在平面PDC内作OM⊥PC交PC于点M,
所以PC⊥平面BOM
连接BM,BM⊥PC,∠BMO是二面角B-PC-D的平面角.
在Rt△BMO中,OB=1, ,
,
 ,
,
所以二面角B-PC-D余弦值为
点评:判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a?α,b?α,a∥b⇒a∥α);③利用面面平行的性质定理(α∥β,a?α⇒a∥β);④利用面面平行的性质(α∥β,a?α,a?,a∥α⇒?a∥β).
(2)要证明平面BDP⊥平面PBC,我们关键是在一个平面内找到一条与另一个平面垂直的直线,观察图形,在平面PBC中,BC可能与平面BDP垂直,故可以其为切入点进行证明.
(3)要求二面角的余弦,要先构造出二面角的平面角,然后利用解三角形的方法,求出这个平面角的余弦值,进而给出二面角的余弦值.
我们也可以构造空间直角坐标系,求出各点的坐标,进行求出相应直线的方向向量和平面的法向量,利用向量法进行求解.
解答:
 解法一:
解法一:证明:建立如图所示的坐标系,
(Ⅰ)A(1,0,0),B(1,1,0),C(0,2,0),D(0,0,0),P(0,0,2)

 ,
, ,
,
设
 ,
,可得

因为PA?平面BDE,
所以PA∥平面BDE
(Ⅱ)因为

所以
 BC⊥BD
BC⊥BD因为PD⊥平面ABCD,所以BC⊥PD
所以BC⊥平面PBD,
所以平面BDP⊥平面PBC.
(Ⅲ)因为AD⊥DC,AD⊥PD
所以
 是平面PDC的法向量,
是平面PDC的法向量, ,设平面PBC的法向量为
,设平面PBC的法向量为 ,
,由
 得:
得: ,
,设二面角B-PC-D为θ,则cosθ=

所以二面角B-PC-D余弦值为
 .
.解法二:
 (Ⅰ)连接AC交BD于G,连接EG,
(Ⅰ)连接AC交BD于G,连接EG,∵AB∥CD
∴
 ,由已知
,由已知 ,
,得
 ,
,∴PA∥EG,
∵EG?平面DEG,PA∉平面DEG
∴PA∥平面DEG.
(Ⅱ)由已知可得,
 ,取CD的中点O,连接BO,ABOD为正方形,
,取CD的中点O,连接BO,ABOD为正方形, ,所以BD2+BC2=CD2由勾股定理的逆定理知BC⊥BD,
,所以BD2+BC2=CD2由勾股定理的逆定理知BC⊥BD,因为BC⊥PD,所以BC⊥平面BDP,所以平面BDP⊥平面PBC
(Ⅲ)BO⊥CD,BO⊥PD,所以BO⊥平面PDC,BO⊥PC
在平面PDC内作OM⊥PC交PC于点M,
所以PC⊥平面BOM
连接BM,BM⊥PC,∠BMO是二面角B-PC-D的平面角.
在Rt△BMO中,OB=1,
 ,
,
 ,
,所以二面角B-PC-D余弦值为

点评:判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a?α,b?α,a∥b⇒a∥α);③利用面面平行的性质定理(α∥β,a?α⇒a∥β);④利用面面平行的性质(α∥β,a?α,a?,a∥α⇒?a∥β).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
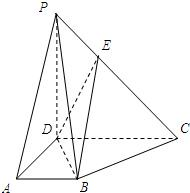 如图:PD⊥平面ABCD,四边形ABCD为直角梯形,AB∥CD,∠ADC=90°,PD=CD=2AD=2AB=2,EC=2PE.
如图:PD⊥平面ABCD,四边形ABCD为直角梯形,AB∥CD,∠ADC=90°,PD=CD=2AD=2AB=2,EC=2PE.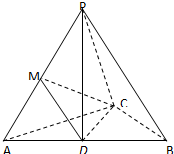 如图,PD⊥平面ABC,AC=BC,D,M分别为AB,PA的中点.求证:
如图,PD⊥平面ABC,AC=BC,D,M分别为AB,PA的中点.求证: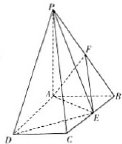 如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F中PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F中PB的中点,点E在边BC上移动.