题目内容
将圆x2+y2-2x+4y=0按向量| a |
| OC |
| OA |
| OB |
| a |
分析:先求出平移后的圆的方程,设出直线的方程,并把它代入圆的方程利用一元二次方程根与系数的关系,求出点C的坐标的解析式,把点C的坐标代入圆的方程,可解得m值,即得点C坐标.
解答: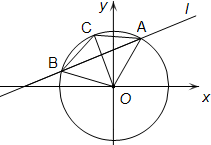 解:将圆的方程x2+y2-2x+4y=0化为(x-1)2+(y+2)2=5,
解:将圆的方程x2+y2-2x+4y=0化为(x-1)2+(y+2)2=5,
∴圆x2+y2-2x+4y=0按向量
=(-1,2)平移后得到圆x2+y2=5,
∵
=
+
=λ
,又|
|=|
|=
,
∴AB⊥OC,
∥
,
∴直线l的斜率k=
,设直线l的方程为y=
x+m,
由
得 5x2+4mx+4m2-20=0,△=16m2-20(4m2-20)>0,
设A(x1,y1),B(x2,y2),则x1+x2=-
,y1+y2=
∴
=(-
,
),∵点C(-
,
)在圆上,∴(-
)2+(
)2=5
解得m=±
,满足△=16m2-20(4m2-20)>0
当m=
时,l的方程为2x-4y+5=0,点C坐标为(-1,2);
当m=-
时,l的方程为2x-4y-5=0,点C坐标为(1,-2).
 解:将圆的方程x2+y2-2x+4y=0化为(x-1)2+(y+2)2=5,
解:将圆的方程x2+y2-2x+4y=0化为(x-1)2+(y+2)2=5,∴圆x2+y2-2x+4y=0按向量
| a |
∵
| OC |
| OA |
| OB |
| a |
| OA |
| OB |
| 5 |
∴AB⊥OC,
| OC |
| a |
∴直线l的斜率k=
| 1 |
| 2 |
| 1 |
| 2 |
由
|
设A(x1,y1),B(x2,y2),则x1+x2=-
| 4m |
| 5 |
| 8m |
| 5 |
∴
| OC |
| 4m |
| 5 |
| 8m |
| 5 |
| 4m |
| 5 |
| 8m |
| 5 |
| 4m |
| 5 |
| 8m |
| 5 |
解得m=±
| 5 |
| 4 |
当m=
| 5 |
| 4 |
当m=-
| 5 |
| 4 |
点评:本题考查向量在几何中的应用,直线和圆相交的性质,一元二次方程根与系数的关系,体现了数形结合的数学思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目