题目内容
6.直线y=x-3与抛物线y2=4x交于A、B两点,过A、B两点向抛物线的准线l作垂线,垂足分别为P、Q,则梯形APQB的面积为( )| A. | 36 | B. | 48 | C. | 56 | D. | 64 |
分析 依题意联立方程组消去y,进而求得交点的坐标,进而根据|AP|,|BQ|和|PQ|的值求得梯形APQB的面积.
解答 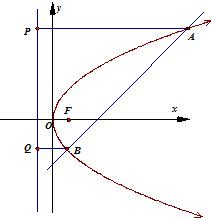 解:直线y=x-3与抛物线y2=4x交于A,B两点,
解:直线y=x-3与抛物线y2=4x交于A,B两点,
过A,B两点向抛物线的准线:x=-1作垂线,垂足分别为P,Q,
联立方程组得$\left\{\begin{array}{l}{{y}^{2}=4x}\\{y=x-3}\end{array}\right.$,
消元得x2-10x+9=0,
解得$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$,和$\left\{\begin{array}{l}{x=9}\\{y=6}\end{array}\right.$,
即有A(9,6),B(1,-2),
即有|AP|=10,|BQ|=2,|PQ|=8,
梯形APQB的面积为$\frac{1}{2}$×(10+2)×8=48,
故选B.
点评 本题主要考查了抛物线与直线的关系.常需要把直线与抛物线方程联立根据韦达定理找到解决问题的途径.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
1.下列说法正确的是( )
| A. | 圆锥的侧面展开图是一个等腰三角形 | |
| B. | 棱柱即是两个底面全等且其余各面都是矩形的多面体 | |
| C. | 任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥 | |
| D. | 通过圆台侧面上一点,有无数条母线 |
14.3对夫妇去看电影,6个人坐成一排,若女性的邻座只能是其丈夫或其他女性,则坐法的种数为( )
| A. | 54 | B. | 60 | C. | 66 | D. | 72 |
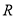 上的不间断函数
上的不间断函数 满足:①当
满足:①当 时,
时, 恒成立;②对任意的
恒成立;②对任意的 都有
都有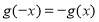 .函数
.函数 满足:对任意的
满足:对任意的 ,都有
,都有 成立,当
成立,当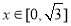 时,
时, ,若关于
,若关于 的不等式
的不等式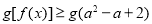 ,对于
,对于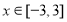 恒成立,则
恒成立,则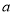 的取值范围为
的取值范围为 展开式的常数项为15,则
展开式的常数项为15,则 ______.
______. 与圆切于点
与圆切于点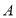 ,过
,过 作直线与圆交于
作直线与圆交于 两点,点
两点,点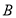 在圆上,且
在圆上,且 .
.
 ;
; ,求
,求 .
.