题目内容
正四面体ABCD的棱长为a，点E，F，G分别是棱AB，AD，DC的中点，则三个数量积：①2| BA |
| AC |
| AD |
| BD |
| FG |
| AC |
分析：根据已知条件逐一求解判断即可求出答案．
解答：解：①2
•
=2•a•a•（-
）=-a2
②2
•
=2•a•a•
=a2
③2
•
=
•
=a2
故答案为：②③
| BA |
| AC |
| 1 |
| 2 |
②2
| AD |
| BD |
| 1 |
| 2 |
③2
| FG |
| AC |
| AC |
| AC |
故答案为：②③
点评：本题考查的知识点是：平面向量的数量积运算
•
=|
|•|
•cosθ；解题的关键是找出参与运算的微量的模和两向量之间的夹角，在求夹角时，一定要注意两个向量是同起点、同终点还是首尾相接．
| a |
| b |
| a |
| b| |
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
正四面体ABCD的棱长为1，G是△ABC的中心，M在线段DG上，且∠AMB=90°，则GM的长为（ ）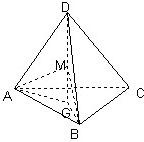
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
（2012•温州一模）如图，直线l⊥平面α，垂足为O，正四面体ABCD的棱长为4，C在平面α内，B是直线l上的动点，则当O到AD的距离为最大时，正四面体在平面α上的射影面积为（ ）