题目内容
已知正四面体ABCD的棱长为a，E为CD上一点，且CE：ED=2：1，则截面△ABE的面积是（ ）
分析：利用正四面体的性质结合余弦定理，求出三角形的底和高即可．
解答：解：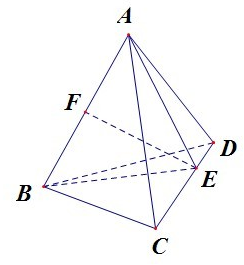
∵CD=a，CE：ED=2：1，
∴CE=
，ED=
，
∴在正三角形ACD中，由余弦定理可知：
AE2=AC2+CE2-2AC•CE•cos∠ACD a2+(
)2-2a?
?
=
a2，
∵三角形BCD和三角形ACD都是正三角形
∴BE=AE，
∴△ABE是等腰三角形
∴在等腰△EAB中，
EF2=AE2-AF2=
a2-(
)2=
a2，
∴S△ABE=
AB?EF=
a?
=
a2．
故选D．
∵CD=a，CE：ED=2：1，∴CE=
| 2a |
| 3 |
| a |
| 3 |
∴在正三角形ACD中，由余弦定理可知：
AE2=AC2+CE2-2AC•CE•cos∠ACD a2+(
| 2a |
| 3 |
| 2a |
| 3 |
| 1 |
| 2 |
| 7 |
| 9 |
∵三角形BCD和三角形ACD都是正三角形
∴BE=AE，
∴△ABE是等腰三角形
∴在等腰△EAB中，
EF2=AE2-AF2=
| 7 |
| 9 |
| a |
| 2 |
| 19 |
| 36 |
∴S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
|
| ||
| 12 |
故选D．
点评：本题主要考查正四面体的应用，以及三角形的面积公式，考查学生的运算能力和分析能力．
练习册系列答案
字词句段篇系列答案
相关题目
已知正四面体ABCD的表面积为S，其四个面的中心分别为E、F、G、H．设四面体EFGH的表面积为T，则
等于（ ）
| T |
| S |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知正四面体ABCD中，M、N分别是BC和AD中点，则异面直线AM和CN所成的角的正切值为（ ）