题目内容
在△ABC中,A(1,2),B(3,4),C(2,k),若∠B为锐角,则实数k的取值范围是( )
分析:由题意算出
=(-2,-2)且
=(-1,k-4).根据B为锐角,可得
•
>0且
、
不平行,由此建立关于k的不等式组,解之即可得到实数k的取值范围.
| BA |
| BC |
| BA |
| BC |
| BA |
| BC |
解答:解:∵A(1,2),B(3,4),C(2,k),
∴
=(-2,-2),
=(-1,k-4).
∵∠B为锐角,
∴
•
>0且
、
不平行,
可得
,解之得k<5且k≠3.
故选:D
∴
| BA |
| BC |
∵∠B为锐角,
∴
| BA |
| BC |
| BA |
| BC |
可得
|
故选:D
点评:本题给出三点A、B、C的坐标,在B为锐角的情况下求参数k的值.着重考查了向量的坐标运算和向量数量积的运算性质等知识,属于基础题.

练习册系列答案
相关题目
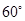 ,b=1,其面积为
,b=1,其面积为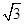 ,则
,则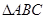 外接圆的半径为
.
外接圆的半径为
.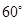 ,b=1,其面积为
,b=1,其面积为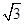 ,则
,则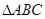 外接圆的半径为
.
外接圆的半径为
.