题目内容
在△ABC中,A(1,1),B(4,5),C(-1,1),则与角A的平分线共线且方向相同的单位向量为
(-
,
)
| ||
| 5 |
2
| ||
| 5 |
(-
,
)
.
| ||
| 5 |
2
| ||
| 5 |
分析:作D点(1,5),则△ADB为直角三角形,∠DAB=arctan
,△CAD为直角三角形,∠CAD=
,由∠CAB=∠CAD+∠DAB,知 tan∠CAB=-
,设E在角平分线上,则∠CAE=
∠CAB,设tan∠CAE=k,则-
=
,由此能求出该单位向量.
| 5 |
| 4 |
| π |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
| 2k |
| 1-k2 |
解答:解:作D点(1,5),则 ①△ADB为直角三角形
∴∠DAB=arctan
,②△CAD为直角三角形
∴∠CAD=
,
∵∠CAB=∠CAD+∠DAB
∴∠CAB=
+arctan
∴tan∠CAB=-
,
设E在角平分线上,则∠CAE=
∠CAB,
设tan∠CAE=k,-
=
,
解之得 k=2 (另一解不合题意,舍去)
即,该角平分线的斜率为 tan(π-∠CAE)=-tan∠CAE=-2.
该向量与之共线且方向相同,
则设其为 (-a,2a),(其中a>0)
又其为单位向量,
则(-a)2+(2a)2=12
解之得 a=
=
,(负值解不合所设,舍去)
则该单位向量为(-
,
).
故答案为:(-
,
).
∴∠DAB=arctan
| 5 |
| 4 |
∴∠CAD=
| π |
| 2 |
∵∠CAB=∠CAD+∠DAB
∴∠CAB=
| π |
| 2 |
| 3 |
| 4 |
∴tan∠CAB=-
| 4 |
| 3 |
设E在角平分线上,则∠CAE=
| 1 |
| 2 |
设tan∠CAE=k,-
| 4 |
| 3 |
| 2k |
| 1-k2 |
解之得 k=2 (另一解不合题意,舍去)
即,该角平分线的斜率为 tan(π-∠CAE)=-tan∠CAE=-2.
该向量与之共线且方向相同,
则设其为 (-a,2a),(其中a>0)
又其为单位向量,
则(-a)2+(2a)2=12
解之得 a=
| 1 | ||
|
| ||
| 5 |
则该单位向量为(-
| ||
| 5 |
2
| ||
| 5 |
故答案为:(-
| ||
| 5 |
2
| ||
| 5 |
点评:本题考查单位向量的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
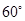 ,b=1,其面积为
,b=1,其面积为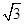 ,则
,则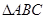 外接圆的半径为
.
外接圆的半径为
.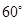 ,b=1,其面积为
,b=1,其面积为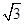 ,则
,则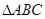 外接圆的半径为
.
外接圆的半径为
.