题目内容
数列{an}满足a1=1,ai+1=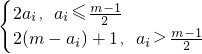 其中m是给定的奇数.若a6=6,则m=________.
其中m是给定的奇数.若a6=6,则m=________.
9
分析:分别令m等于正奇数1,3,5,7,9,求出数列的前6项,经检验,m=9时满足第6项等于6,再由m是给定的奇数,
从而求得m的值.
解答:∵数列{an}满足a1=1,若a1>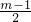 ,且m为奇数,那么m=1.此时求得a2=1,
,且m为奇数,那么m=1.此时求得a2=1,
同理求得a6=1,这与已知矛盾,故m≠1.
若m=3,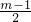 =1,由于a2=2,a3=3,a4=1,a5=2,a6=3,与题目矛盾,则m≠3.
=1,由于a2=2,a3=3,a4=1,a5=2,a6=3,与题目矛盾,则m≠3.
若m=5,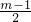 =2,由于a2=2,a3=4,a4=3,a5=5,a6=1,与题目矛盾,则m≠5.
=2,由于a2=2,a3=4,a4=3,a5=5,a6=1,与题目矛盾,则m≠5.
若m=7,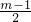 =3,由于a2=2,a3=4,a4=7,a5=1,a6=2,与题目矛盾,则m≠7.
=3,由于a2=2,a3=4,a4=7,a5=1,a6=2,与题目矛盾,则m≠7.
若m=9,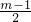 =4,由于a2=2,a3=4,a4=8,a5=3,a6=6,满足题中的条件,故m=9.
=4,由于a2=2,a3=4,a4=8,a5=3,a6=6,满足题中的条件,故m=9.
因为m是给定的奇数,所以m只能等于9,不可能是别的奇数.
故答案为 9.
点评:本题主要考查利用数列的递推关系求数列的前几项,数列的函数特性的应用,属于难题.
分析:分别令m等于正奇数1,3,5,7,9,求出数列的前6项,经检验,m=9时满足第6项等于6,再由m是给定的奇数,
从而求得m的值.
解答:∵数列{an}满足a1=1,若a1>
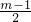 ,且m为奇数,那么m=1.此时求得a2=1,
,且m为奇数,那么m=1.此时求得a2=1,同理求得a6=1,这与已知矛盾,故m≠1.
若m=3,
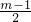 =1,由于a2=2,a3=3,a4=1,a5=2,a6=3,与题目矛盾,则m≠3.
=1,由于a2=2,a3=3,a4=1,a5=2,a6=3,与题目矛盾,则m≠3.若m=5,
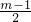 =2,由于a2=2,a3=4,a4=3,a5=5,a6=1,与题目矛盾,则m≠5.
=2,由于a2=2,a3=4,a4=3,a5=5,a6=1,与题目矛盾,则m≠5.若m=7,
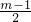 =3,由于a2=2,a3=4,a4=7,a5=1,a6=2,与题目矛盾,则m≠7.
=3,由于a2=2,a3=4,a4=7,a5=1,a6=2,与题目矛盾,则m≠7.若m=9,
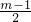 =4,由于a2=2,a3=4,a4=8,a5=3,a6=6,满足题中的条件,故m=9.
=4,由于a2=2,a3=4,a4=8,a5=3,a6=6,满足题中的条件,故m=9.因为m是给定的奇数,所以m只能等于9,不可能是别的奇数.
故答案为 9.
点评:本题主要考查利用数列的递推关系求数列的前几项,数列的函数特性的应用,属于难题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目