题目内容
设O为坐标原点,A(1,1),若点B满足
,则
在
上投影的最小值为( )
|
| OB |
| OA |
| A、2 | ||||
B、2
| ||||
C、
| ||||
D、
|
分析:利用向量的数量积求出目标函数,作出不等式组表示的可行域,作出与目标函数平行的直线,将直线平行由图知当与圆相切时,z最小.利用圆心到直线的距离等于半径求出z值.
解答:解:设B(x,y),
画出
表示的平面区域,如图所示:
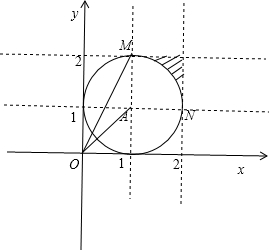
点B为图中的阴影部分中的任一点,由题意可知:
当B与图中的M或N重合时,cos∠AOB最小,且|
|也最小,
在△AOM中,|OA|=
=
,|OM|=
=
,|AM|=2-1=1,
则根据余弦定理得:cos∠AOM=
=
,
由此时B与M重合得到:cos∠AOB=
,|
|=
,
则
在
上投影的最小值为|
|cos∠AOB=
×
=
.
故选D
画出
|

点B为图中的阴影部分中的任一点,由题意可知:
当B与图中的M或N重合时,cos∠AOB最小,且|
| OB |
在△AOM中,|OA|=
| 1+1 |
| 2 |
| 1+22 |
| 5 |
则根据余弦定理得:cos∠AOM=
| |OM|2+|OA|2-|AM|2 |
| 2|OM|•|OA| |
3
| ||
| 10 |
由此时B与M重合得到:cos∠AOB=
3
| ||
| 10 |
| OB |
| 5 |
则
| OB |
| OA |
| OB |
| 5 |
3
| ||
| 10 |
3
| ||
| 2 |
故选D
点评:本题考查了直线与圆相交的性质,涉及的知识有平面向量射影的定义,不等式组构成的平面区域,勾股定理,以及余弦定理,利用了数形结合的思想,要求学生根据题意画出相应的图形,借助图形找出射影最小值时点B的位置是解本题的关键.

练习册系列答案
相关题目