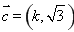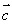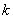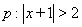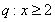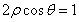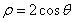题目内容
已知椭圆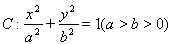 的离心率为
的离心率为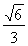 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为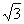 .
.
(1)求椭圆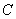 的方程;
的方程;
(2)设不与坐标轴平行的直线 与椭圆
与椭圆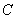 交于
交于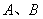 两点,坐标原点
两点,坐标原点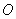 到直线
到直线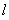 的距离为
的距离为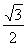 ,求
,求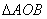 面积的最大值.
面积的最大值.
(1)椭圆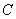 的方程为
的方程为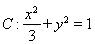 ;(2)
;(2)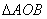 面积的最大值为
面积的最大值为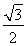 .
.
【解析】
试题分析:(1) 求椭圆的方程,可利用待定系数法求出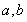 的值即可,依题意,
的值即可,依题意,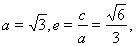 可得:
可得: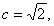 ,从而可得
,从而可得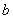 的值,即得椭圆的方程;(2)由于直线l是任意的,故可设其方程为
的值,即得椭圆的方程;(2)由于直线l是任意的,故可设其方程为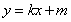 .根据坐标原点
.根据坐标原点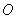 到直线
到直线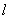 的距离为
的距离为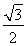 ,可得
,可得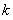 与
与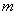 的关系式,从而将双参数问题变为单参数问题.将
的关系式,从而将双参数问题变为单参数问题.将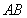 作为底边,则
作为底边,则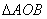 的高为常数
的高为常数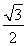 ,所以要使
,所以要使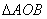 的面积最大,就只需
的面积最大,就只需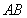 边最大.将
边最大.将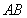 用
用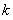 或
或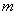 表示出来便可求得
表示出来便可求得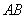 的最大值,从而求得
的最大值,从而求得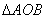 的面积的最大值.
的面积的最大值.
试题解析:(1)依题意,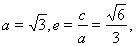 可得:
可得: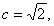
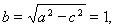
所以,椭圆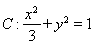 ;
;
(2)坐标原点 到直线
到直线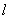 的距离为
的距离为 ,所以,
,所以,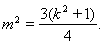
联立 可得:
可得: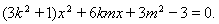
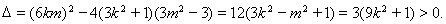
所以, 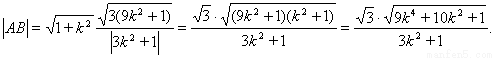
由题意,得: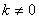 ,令
,令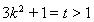 ,所以
,所以
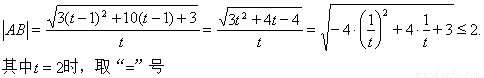 ,
,
所以,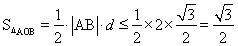 .
.
考点:椭圆方程,直线与圆锥曲线;点到直线的距离公式,基本不等式;弦长及三角形的面积.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目