题目内容
设函数f(x)=kax-a-x(a>0且a≠1,k∈R),f(x)是定义域为R上的奇函数.(1)求k的值,并证明当a>1时,函数f(x)是R上的增函数;
(2)已知
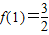 ,函数g(x)=a2x+a-2x-4f(x),x∈[1,2],求g(x)的值域;
,函数g(x)=a2x+a-2x-4f(x),x∈[1,2],求g(x)的值域;(3)若a=4,试问是否存在正整数λ,使得f(2x)≥λ•f(x)对
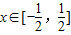 恒成立?若存在,请求出所有的正整数λ;若不存在,请说明理由.
恒成立?若存在,请求出所有的正整数λ;若不存在,请说明理由.
【答案】分析:(1)由f(x)为R上的奇函数可得f(0)=0,解得k值,然后进行检验,根据增函数的定义即可证明其单调性;
(2)由f(1)= 可求得a值,则g(x)=)=(2x-2-x)2-4(2x-2-x)+2,令t=2x-2-x(1≤x≤2),由此g(x)可化为关于t的二次函数,求出t的范围,根据二次函数的性质即可求得g(x)的最小值、最大值,从而得其值域;
可求得a值,则g(x)=)=(2x-2-x)2-4(2x-2-x)+2,令t=2x-2-x(1≤x≤2),由此g(x)可化为关于t的二次函数,求出t的范围,根据二次函数的性质即可求得g(x)的最小值、最大值,从而得其值域;
(3)按照x=0,0<x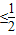 ,-
,-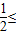 x<0三种情况,分离出参数λ后转化为函数最值解出λ相应范围,最后取其交集即可;
x<0三种情况,分离出参数λ后转化为函数最值解出λ相应范围,最后取其交集即可;
解答:解:(1)∵f(x)=kax-a-x是定义域为R上的奇函数,
∴f(0)=0,得k=1.
此时,f(x)=ax-a-x,f(-x)=a-x-ax=-f(x),即f(x)是R上的奇函数.
设x2>x1,则f(x2)-f(x1)=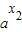 -
-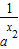 -(
-(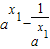 )=(
)=(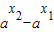 )(1+
)(1+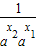 ),
),
∵a>1,x2>x1,∴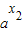 >
>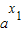 ,
,
∴f(x2)-f(x1)>0,
∴f(x)在R上为增函数.
(2)∵f(1)= ,∴a-
,∴a-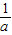 =
= ,即2a2-3a-2=0,
,即2a2-3a-2=0,
解得a=2或a=- (舍去),
(舍去),
∴g(x)=22x+2-2x-4(2x-2-x)=(2x-2-x)2-4(2x-2-x)+2,
令t=2x-2-x(1≤x≤2),
由(1)知t=2x-2-x[1,2]上为增函数,∴t∈[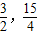 ],
],
∴g(x)=Φ(t)=t2-4t+2=(t-2)2-2,
当t=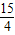 时,g(x)有最大值
时,g(x)有最大值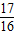 ,当t=2时,g(x)有最小值-2,
,当t=2时,g(x)有最小值-2,
∴g(x)的值域[-2, ].
].
(3)f(2x)=42x-4-2x=(4x+4-x)•(4x-4-x),f(x)=4x-4-x,
假设存在满足条件的正整数λ,则(4x+4-x)•(4x-4-x)≥λ•(4x-4-x),
①当x=0时,λ∈R;
②当x 时,4x-4-x>0,则λ≤4x+4-x,
时,4x-4-x>0,则λ≤4x+4-x,
令μ=4x,则μ∈(1,2],易证z=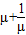 在(1,2]上是增函数,
在(1,2]上是增函数,
则λ≤z(1)=2;
③当x 时,4x-4-x<0,则
时,4x-4-x<0,则 ,
,
令μ=4x,则 ,易证z=
,易证z= 在[
在[ ,1)上是减函数,
,1)上是减函数,
所以λ≥z( )=
)= ,
,
综上所述,知不存在正整数λ满足题意.
点评:本题是对函数单调性和奇偶性的综合考查.对函数单调性和奇偶性的综合考查的一般出题形式是解不等式的题,解题方法是先利用奇偶性进行转化,再利用单调性解不等式.
(2)由f(1)=
 可求得a值,则g(x)=)=(2x-2-x)2-4(2x-2-x)+2,令t=2x-2-x(1≤x≤2),由此g(x)可化为关于t的二次函数,求出t的范围,根据二次函数的性质即可求得g(x)的最小值、最大值,从而得其值域;
可求得a值,则g(x)=)=(2x-2-x)2-4(2x-2-x)+2,令t=2x-2-x(1≤x≤2),由此g(x)可化为关于t的二次函数,求出t的范围,根据二次函数的性质即可求得g(x)的最小值、最大值,从而得其值域;(3)按照x=0,0<x
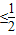 ,-
,-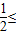 x<0三种情况,分离出参数λ后转化为函数最值解出λ相应范围,最后取其交集即可;
x<0三种情况,分离出参数λ后转化为函数最值解出λ相应范围,最后取其交集即可;解答:解:(1)∵f(x)=kax-a-x是定义域为R上的奇函数,
∴f(0)=0,得k=1.
此时,f(x)=ax-a-x,f(-x)=a-x-ax=-f(x),即f(x)是R上的奇函数.
设x2>x1,则f(x2)-f(x1)=
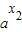 -
-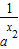 -(
-(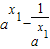 )=(
)=(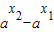 )(1+
)(1+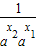 ),
),∵a>1,x2>x1,∴
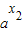 >
>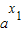 ,
,∴f(x2)-f(x1)>0,
∴f(x)在R上为增函数.
(2)∵f(1)=
 ,∴a-
,∴a-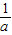 =
= ,即2a2-3a-2=0,
,即2a2-3a-2=0,解得a=2或a=-
 (舍去),
(舍去),∴g(x)=22x+2-2x-4(2x-2-x)=(2x-2-x)2-4(2x-2-x)+2,
令t=2x-2-x(1≤x≤2),
由(1)知t=2x-2-x[1,2]上为增函数,∴t∈[
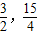 ],
],∴g(x)=Φ(t)=t2-4t+2=(t-2)2-2,
当t=
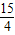 时,g(x)有最大值
时,g(x)有最大值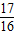 ,当t=2时,g(x)有最小值-2,
,当t=2时,g(x)有最小值-2,∴g(x)的值域[-2,
 ].
].(3)f(2x)=42x-4-2x=(4x+4-x)•(4x-4-x),f(x)=4x-4-x,
假设存在满足条件的正整数λ,则(4x+4-x)•(4x-4-x)≥λ•(4x-4-x),
①当x=0时,λ∈R;
②当x
 时,4x-4-x>0,则λ≤4x+4-x,
时,4x-4-x>0,则λ≤4x+4-x,令μ=4x,则μ∈(1,2],易证z=
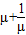 在(1,2]上是增函数,
在(1,2]上是增函数,则λ≤z(1)=2;
③当x
 时,4x-4-x<0,则
时,4x-4-x<0,则 ,
,令μ=4x,则
 ,易证z=
,易证z= 在[
在[ ,1)上是减函数,
,1)上是减函数,所以λ≥z(
 )=
)= ,
,综上所述,知不存在正整数λ满足题意.
点评:本题是对函数单调性和奇偶性的综合考查.对函数单调性和奇偶性的综合考查的一般出题形式是解不等式的题,解题方法是先利用奇偶性进行转化,再利用单调性解不等式.

练习册系列答案
相关题目
 如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k. 如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.