题目内容
已知函数![]() .
.
(Ⅰ)若![]() 值点,求a的值;
值点,求a的值;
(Ⅱ)求证:当0<a≤2时,f(x)在![]() 上是增函数;
上是增函数;
(Ⅲ)若对任意的![]() ,总存在
,总存在![]() ,使不等式
,使不等式![]() 成立,求实数m的取值范围.
成立,求实数m的取值范围.
解: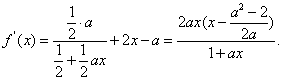
(Ⅰ)由已知得:![]() 且
且![]()
![]() ………………3分
………………3分
(Ⅱ)当![]() 时,
时,![]() ,
,
![]() 故当
故当![]() 时,
时,![]()
又![]() 故
故![]() 在
在![]() 上是增函数. ……………7分
上是增函数. ……………7分
(Ⅲ)当![]() 时,由(2)知,
时,由(2)知,![]() 在
在![]() 上的最小值为
上的最小值为![]() 故问题等价于:
故问题等价于:
对任意的![]() ,不等式
,不等式![]() 恒成立.……8分
恒成立.……8分
记![]() ,
,
则![]()
当![]() 时,
时,![]() 在区间
在区间![]() 上递减,此时,
上递减,此时,![]()
![]() 时不可能使
时不可能使![]() 恒成立,故必有
恒成立,故必有![]() …………10分
…………10分
.![]()
若![]() 可知
可知![]() 在区间
在区间![]() 上递减,在此区间上,有
上递减,在此区间上,有![]() 与
与![]() 恒成立矛盾,故
恒成立矛盾,故![]() 此时
此时![]()
![]() 在
在![]() 上递增,且恒有
上递增,且恒有![]() 满足题设要求,
满足题设要求,
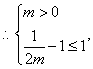 即
即![]() ,即实数
,即实数![]() 的取值范围为
的取值范围为![]() . ……………13分
. ……………13分

练习册系列答案
相关题目
 ,若
,若 ,则实数
,则实数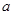 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
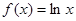 ,若
,若
 在点
在点 处的切线方程;
处的切线方程; 在区间
在区间 上有两个零点,求实数b的取值范围;
上有两个零点,求实数b的取值范围;
 ,若
,若 为奇函数,则
为奇函数,则 ▲
▲
 ,若
,若 ,
, ,则
,则  (B)
(B)
 (D)
(D) 与
与 的大小不能确定
的大小不能确定