题目内容
(本小题14分)
已知函数 ,若
,若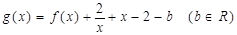
(1)求曲线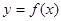 在点
在点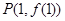 处的切线方程;
处的切线方程;
(2)若函数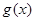 在区间
在区间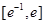 上有两个零点,求实数b的取值范围;
上有两个零点,求实数b的取值范围;
(3)当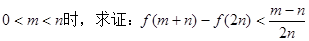
【答案】
(1)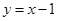 ;(2)(1,
;(2)(1,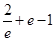 ] ;(3)证明详见解析.
] ;(3)证明详见解析.
【解析】
试题分析:(1)先求导数,再求切线的斜率,由点斜式可得切线方程;(2)先求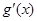 ,然后确定函数
,然后确定函数
g(x)的单调区间,找到满足函数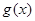 在区间
在区间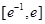 上有两个零点d的条件,解之即可;(3)欲证原不等式可转化为证
上有两个零点d的条件,解之即可;(3)欲证原不等式可转化为证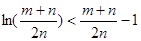 ,在构造函数
,在构造函数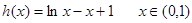 ,由函数h(x)的单调性可证的
,由函数h(x)的单调性可证的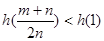 <0,即可得证.
<0,即可得证.
试题解析:(1)因为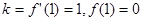 ,
,
所以曲线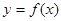 在点
在点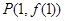 处的切线方程为
处的切线方程为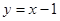
(2) =
=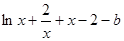 ,(x>0)
,(x>0)
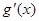 =
=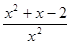 ,由
,由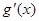 >0得x>1, 由
>0得x>1, 由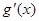 <0得0<x<1.
<0得0<x<1.
所以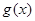 的单调递增区间是(1,+
的单调递增区间是(1,+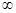 ),单调递减区间(0, 1)
),单调递减区间(0, 1)
x=1时,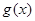 取得极小值
取得极小值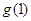 .
.
因为函数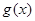 在区间
在区间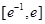 上有两个零点,所以
上有两个零点,所以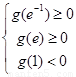 ,解得
,解得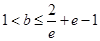 ,
,
所以b的取值范围是(1,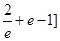
(3)当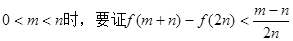
即证: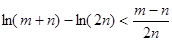
即证: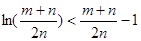
构造函数: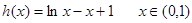
当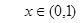 时,
时,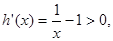
所以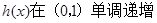 ,
,
又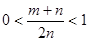 ,所以
,所以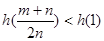
即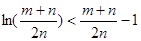
所以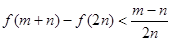
考点:1.导数的几何意义;2.函数的零点;3.导数的应用.

练习册系列答案
相关题目
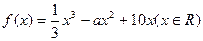 .
.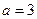 ,点P为曲线
,点P为曲线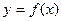 上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;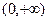 上为单调增函数,试求
上为单调增函数,试求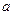 的取值范围.
的取值范围.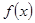 满足:
满足: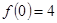 ,
,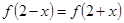 ,且该函数的最小值为1.
,且该函数的最小值为1. =
= 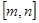 .(其中
.(其中 ). 问是否存在这样的两个实数
). 问是否存在这样的两个实数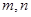 ,使得函数
,使得函数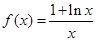
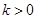 且函数
且函数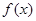 在区间
在区间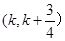 上存在极值,求实数
上存在极值,求实数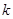 的取值范围;
的取值范围;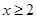 时,不等式
时,不等式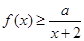 恒成立,求实数
恒成立,求实数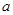 的取值范围;
的取值范围;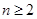 ,
,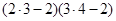 ……
……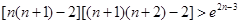 .
.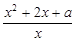 ,x∈[1,+∞
,x∈[1,+∞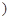
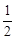 时,求函数f(x)的最小值
时,求函数f(x)的最小值 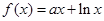
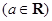 .
.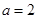 ,求曲线
,求曲线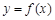 在
在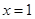 处切线的斜率;
处切线的斜率; 的单调区间;
的单调区间;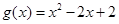 ,若对任意
,若对任意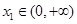 ,均存在
,均存在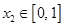 ,使得
,使得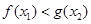 ,求
,求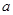 的取值范围。
的取值范围。