题目内容
如果一个几何体的三视图如图所示,则此几何体的表面积是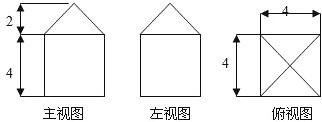
分析:先判断三视图复原的结合体的形状,上部是正四棱锥,下部是正方体,确定棱长,可求结合体的表面积.
解答:解:三视图复原的结合体,上部是正四棱锥,底面棱长为4,
高为2,下部是正方体,底面棱长为4,
所以结合体的表面积是:5×42+
×16×2
=80+16
故答案为:80+16
高为2,下部是正方体,底面棱长为4,
所以结合体的表面积是:5×42+
| 1 |
| 2 |
| 2 |
| 2 |
故答案为:80+16
| 2 |
点评:本题考查三视图求结合体的表面积,考查空间想象能力,计算能力,是基础题.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
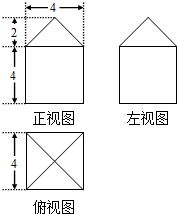 如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的体积是( )
如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的体积是( )| A、96cm3 | ||
| B、80cm3 | ||
C、(80+16
| ||
D、
|
 如果一个几何体的三视图如图(单位长度:cm),则此几何体的体积是( )
如果一个几何体的三视图如图(单位长度:cm),则此几何体的体积是( ) 如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的体积是
如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的体积是 如果一个几何体的三视图如图所示,则此几何体的体积是( )
如果一个几何体的三视图如图所示,则此几何体的体积是( )