题目内容
【题目】已知中心在原点 ![]() ,焦点在
,焦点在 ![]() 轴上的椭圆,离心率
轴上的椭圆,离心率 ![]() ,且椭圆过点
,且椭圆过点 ![]() .
.
(1)求椭圆的方程;
(2)设椭圆左、右焦点分别为 ![]() ,过
,过 ![]() 的直线
的直线 ![]() 与椭圆交于不同的两点
与椭圆交于不同的两点 ![]() ,则
,则 ![]() 的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
【答案】
(1)解:由题意可设椭圆方程为 ![]() .
.
则 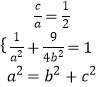 ,
,
解得: ![]() 椭圆方程为
椭圆方程为 ![]() ,
,
(2)解:设 ![]() ,不妨
,不妨 ![]() ,设
,设 ![]() 的内切圆的半径
的内切圆的半径 ![]() ,
,
则 ![]() 的周长为
的周长为 ![]() 因此
因此 ![]() 最大,
最大,![]() 就最大,
就最大,
由题知,直线 ![]() 的斜率不为零,可设直线
的斜率不为零,可设直线 ![]() 的方程为
的方程为 ![]() ,
,
由 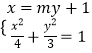 得
得 ![]() ,
,
得 ![]()
则 ![]() ,
,
令 ![]() ,可知
,可知 ![]() ,则
,则 ![]()
![]() ,
,
令 ![]() ,则
,则 ![]() ,当
,当 ![]() 时,
时, ![]() ,
, ![]() 在
在 ![]() 上单调递增,有
上单调递增,有 ![]() ,
,
即当 ![]() 时,
时, ![]() ,这时所求内切圆面积的最大值为
,这时所求内切圆面积的最大值为 ![]() .
.
故直线 ![]() 内切圆面积的最大值为
内切圆面积的最大值为 ![]() .
.
【解析】(1)根据椭圆的简单性质可求出a、b的值从而得到椭圆的方程。(2)由已知可得到a的值根据三角形面积最大R 就最大,设出直线的方程与椭圆联立即可表示出Δ F1AB 的面积,再利用换元法借助导数的性质求出其增减性进而可求出其内切圆面积的最大值。

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目