题目内容
给出下列命题:
①半径为2,圆心角的弧度数为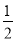 的扇形面积为
的扇形面积为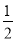 ;
;
②在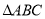 中,
中, 的充要条件是
的充要条件是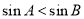 ;
;
③在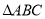 中,若
中,若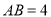 ,
,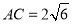 ,
,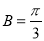 ,则
,则 为钝角三角形;
为钝角三角形;
④函数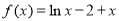 在区间
在区间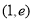 上存在零点.
上存在零点.
其中真命题的序号是__________.
练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
题目内容
给出下列命题:
①半径为2,圆心角的弧度数为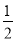 的扇形面积为
的扇形面积为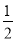 ;
;
②在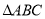 中,
中, 的充要条件是
的充要条件是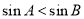 ;
;
③在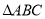 中,若
中,若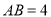 ,
,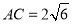 ,
,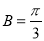 ,则
,则 为钝角三角形;
为钝角三角形;
④函数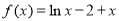 在区间
在区间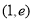 上存在零点.
上存在零点.
其中真命题的序号是__________.
 发散思维新课堂系列答案
发散思维新课堂系列答案