题目内容
(本题满分12分)设f(x)=x3+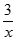 求函数f(x)的单调区间及其极值;
求函数f(x)的单调区间及其极值;
【答案】
增(-∞,-1),(1,+∞) 减(-1,0),(0,1) 极大-4,极小4
【解析】
试题分析:定义域为(-∞,0)∪(0,+∞)(2分)f′(x)=3x2- 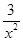
令f'(x)=0,得x=±1
当x变化时,f'(x),f(x)的变化情况如下
|
x |
(-∞,-1) |
-1 |
(-1,0) |
0 |
(0,1) |
1 |
(1,+∞) |
|
f'(x) |
+ |
|
- |
|
- |
|
+ |
|
f(x) |
↗ |
-4 |
↘ |
|
↘ |
4 |
↗ |
所以函数f(x)的增区间(-∞,-1),(1,+∞);减区间(-1,0),(0,1);
极大值为f(-1)=-4,极小值为f(1)=4。
考点:本题主要考查利用导数研究函数的单调性及最值。
点评:常见题型。表解法是利用导数研究函数单调性、求极值的较好方法,直观清晰。

练习册系列答案
相关题目
 :实数
:实数 满足
满足 , 命题
, 命题 :实数
:实数 .
. 为真,求实数
为真,求实数 .
. 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,其中
,其中 。
。 时,求不等式
时,求不等式 的解集;
的解集;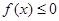 的解集为
的解集为 ,求a的值。
,求a的值。
 与
与 垂直,求
垂直,求 的值
的值  的最大值;
的最大值;  ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 与
与 、
、 两点,且
两点,且 ,
, ,
, 成等差数列,
成等差数列, 满足
满足 ,求
,求