题目内容
(本题满分12分)
设 ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 斜率为1的直线
斜率为1的直线 与
与 相交于
相交于 、
、 两点,且
两点,且 ,
, ,
, 成等差数列,
成等差数列,
(Ⅰ)求 的离心率;
的离心率;
(Ⅱ)设点 满足
满足 ,求
,求 的方程。
的方程。
【答案】
18.解:(Ⅰ)由椭圆定义知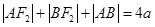 ,
,
又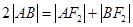 , 得
, 得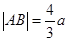
设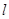 的方程为
的方程为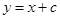 ,其中
,其中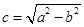 。
。
设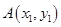 ,
,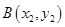 ,
,
方程组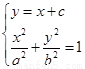 联立消去
联立消去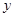 ,化简得
,化简得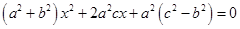
则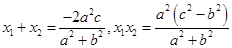
因为直线AB斜率为1,所以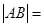
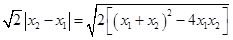
所以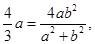 故
故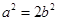
所以E的离心率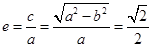
(Ⅱ)设AB的中点为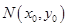 ,由(I)知
,由(I)知
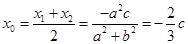 ,
,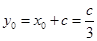 。
。
由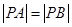 ,得
,得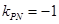 ,即
,即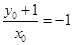
得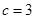 ,从而
,从而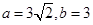 故椭圆E的方程为
故椭圆E的方程为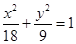 。
。
【解析】略

练习册系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面