题目内容
如图所示:边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直且DE=![]() ,ED//AF且∠DAF=90°。
,ED//AF且∠DAF=90°。
(1)求BD和面BEF所成的角的余弦;
|
|
|
答案:(1)因为AC、AD、AB两两垂直,建立如图坐标系,
则B(2,0,0),D(0,0,2),
E(1,1,2),F(2,2,0),
则![]()
设平面BEF的法向量![]()
![]() ,则可取
,则可取![]() ,
,
∴向量![]() 所成角的余弦为
所成角的余弦为
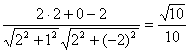 。
。
即BD和面BEF所成的角的余弦![]() 。
。
(2)假设线段EF上存在点P使过P、A、C三点的平面和直线DB垂直,不妨设EP与PF的比值为m,则P点坐标为![]()
则向量![]()
![]() ,向量
,向量![]()
![]()
所以![]() 。
。
点评:本题考查了线线关系,线面关系及其相关计算,本题采用探索式、开放式设问方式,对学生灵活运用知识解题提出了较高要求。

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
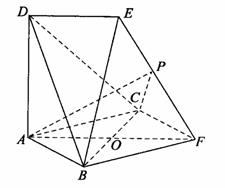

 如图所示,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2
如图所示,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2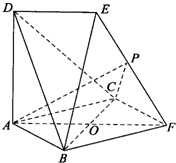 如图所示:边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直且DE=
如图所示:边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直且DE= 如图所示,边长为2的等边△
如图所示,边长为2的等边△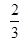 ,则阴影区域的面积为( )
,则阴影区域的面积为( )
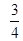 B.
B.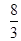 C.
C.