题目内容
 如图所示,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2
如图所示,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2| 2 |
(1)证明:AM⊥PM;
(2)求二面角P-AM-D的大小.
分析:(1)利用勾股定理的逆定理、线面与面面垂直的判定和性质定理即可证明;
(2)利用三垂线定理或线面垂直的性质定理及二面角的定义、正切函数即可得出.
(2)利用三垂线定理或线面垂直的性质定理及二面角的定义、正切函数即可得出.
解答:(1)证明:如图所示,取CD的中点E,连接PE,EM,EA,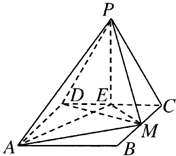
∵△PCD为正三角形,
∴PE⊥CD,PE=PDsin∠PDE=2sin60°=
.
∵平面PCD⊥平面ABCD,
∴PE⊥平面ABCD,而AM?平面ABCD,∴PE⊥AM.
∵四边形ABCD是矩形,
∴△ADE,△ECM,△ABM均为直角三角形,
由勾股定理可求得EM=
,AM=
,AE=3,
∴EM2+AM2=AE2.∴AM⊥EM.
又PE∩EM=E,∴AM⊥平面PEM,∴AM⊥PM.
(2)解:由(1)可知:EM⊥AM,PM⊥AM,
∴∠PME是二面角P-AM-D的平面角.
在Rt△PEM中,tan∠PME=
=
=1,∴∠PME=45°.
∴二面角P-AM-D的大小为45°.

∵△PCD为正三角形,
∴PE⊥CD,PE=PDsin∠PDE=2sin60°=
| 3 |
∵平面PCD⊥平面ABCD,
∴PE⊥平面ABCD,而AM?平面ABCD,∴PE⊥AM.
∵四边形ABCD是矩形,
∴△ADE,△ECM,△ABM均为直角三角形,
由勾股定理可求得EM=
| 3 |
| 6 |
∴EM2+AM2=AE2.∴AM⊥EM.
又PE∩EM=E,∴AM⊥平面PEM,∴AM⊥PM.
(2)解:由(1)可知:EM⊥AM,PM⊥AM,
∴∠PME是二面角P-AM-D的平面角.
在Rt△PEM中,tan∠PME=
| PE |
| EM |
| ||
|
∴二面角P-AM-D的大小为45°.
点评:熟练掌握线面与面面垂直的判定和性质定理、三垂线定理、二面角的定义、正切函数及勾股定理的逆定理是解题的关键.

练习册系列答案
相关题目
如图所示:边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直且DE=![]() ,ED//AF且∠DAF=90°。
,ED//AF且∠DAF=90°。
(1)求BD和面BEF所成的角的余弦;
|
|
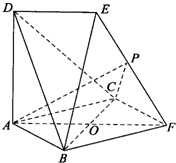 如图所示:边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直且DE=
如图所示:边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直且DE= 如图所示,边长为2的等边△
如图所示,边长为2的等边△
 ,则阴影区域的面积为( )
,则阴影区域的面积为( )
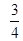 B.
B.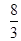 C.
C.