题目内容
圆O1的方程为x2+(y+1)2=4,圆O2的圆心为O2(2,1).(1)若⊙O2与⊙O1外切,求圆O2的方程,并求内公切线方程;
(2)若⊙O2与⊙O1交于A、B两点,且|AB|=2![]() ,求⊙O2的方程.
,求⊙O2的方程.
解:(1)由两圆外切,所以|O1O2|=r1+r2.
所以r2=|O1O2|-r1=2(![]() -1).
-1).
故圆O2的方程是(x-2)2+(y-1)2=4(![]() -1)2.
-1)2.
两圆方程相减,即得两圆内公切线的方程为x+y+1-2![]() =0.
=0.
(2)设圆O2的方程为(x-2)2+(y-1)2=r22.
因为圆O1的方程为x2+(y+1)2=4,
所以两圆公共弦AB所在直线方程为4x+4y+r22-8=0.
作O1H⊥AB,则|AH|=![]() |AB|=
|AB|=![]() ,
,
在Rt△AO1H中,
|O1H|=![]() =
=![]() ,
,
由圆心O1到AB的距离d=![]() =
=![]() ,
,
所以r22=4或r22=20.
所以⊙O2的方程为(x-2)2+(y-1)2=4或(x-2)2+(y-1)2=20.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
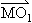 ⊥
⊥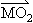 ?若存在,求出M点的坐标;若不存在,请说明理由.
?若存在,求出M点的坐标;若不存在,请说明理由.