题目内容
已知圆O1的方程为x2+y2-2x=0,一个动圆P与圆O1外切且过定点O2(-1,0).
(1)求动圆圆心P点的轨迹方程;
(2)所求P点轨迹上是否存在一点M,使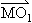 ⊥
⊥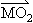 ?若存在,求出M点的坐标;若不存在,请说明理由.
?若存在,求出M点的坐标;若不存在,请说明理由.
答案:
解析:
解析:
|
(1)圆O1即(x-1)2+y2=1,∴|PO1|-|PO2|=1,所求轨迹是以(-1,0),(1,0)为焦点、实轴长为1的双曲线的左支,方程为 (2)设M(x1,y1),则(x1-1)(x1+1)+ ∴ ∴ |

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
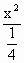 -
-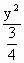 =1(x≤
=1(x≤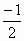 ).
).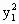 =0.
=0.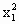 +
+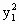 -1=0与4
-1=0与4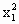 -
-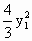 =1联立.
=1联立.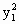 =(
=(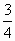 )2,由x1≤
)2,由x1≤ ,得所求M存在,其坐标为(-
,得所求M存在,其坐标为(-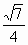 ,±
,±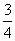 ).
). A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲 (2012•徐州模拟)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,
(2012•徐州模拟)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,