题目内容
已知点D(-6,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过T(-1,0)作直线与轨迹C交于A、B两点,若在x轴上存在一点E(x0,0),使△ABE为等边三角形,求x0的值.
解:(1)设M(x,y),P(0,y′),Q(x′,0)(x′>0),
∵![]() =
=![]()
![]() 故由
故由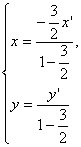 解得
解得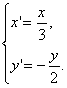 ∴
∴![]()
再由![]() =0,得(6,
=0,得(6,![]() )·(x,
)·(x,![]() y)=0,
y)=0,
6x-![]() y2=0,∴y2=8x(x>0).
y2=0,∴y2=8x(x>0).
故动点M的轨迹C是以(0,0)为顶点、(2,0)为焦点的抛物线(除去原点).
(2)设过T(-1,0)的直线l的方程为y=k(x+1)(k≠0),
代入y2=8x,得k2x2+2(k2-4)x+k2=0.
设A(x1,y1),B(x2,y2),则x1+x2=![]() ,x1x2=1,∴AB中点为(
,x1x2=1,∴AB中点为(![]() ).线段AB的中垂线方程为y
).线段AB的中垂线方程为y![]() ,令y=0,得x0=
,令y=0,得x0=![]() +4=3+
+4=3+![]() .
.
∴E(3+![]() ,0).∵△ABE为等边三角形,故点E到AB的距离为d=
,0).∵△ABE为等边三角形,故点E到AB的距离为d=![]() |AB|.而|AB|=
|AB|.而|AB|=![]() |x2-x1|=
|x2-x1|=![]() ·
·![]() ,
,
故d=![]() .
.
又E到直线y=k(x+1),即kx-y+k=0的距离为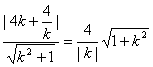 ,
,
由![]() ,解得k=±
,解得k=±![]() .∴3+
.∴3+![]() =6
=6![]() .
.
∴E点坐标为(6![]() ,0).
,0).

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目