题目内容
10.已知{an}是各项均为正数的等比数列,{bn}是等差数列,且a1=b1=1,b2+b3=2a3,a5-3b2=7.(Ⅰ)求{an}和{bn}的通项公式;
(Ⅱ)设cn=anbn,n∈N*,求数列{cn}的前n项和.
分析 (Ⅰ)设出数列{an}的公比和数列{bn}的公差,由题意列出关于q,d的方程组,求解方程组得到q,d的值,则等差数列和等比数列的通项公式可求;
(Ⅱ)由题意得到${c}_{n}=(2n-1)•{2}^{n-1}$,然后利用错位相减法求得数列{cn}的前n项和.
解答 解:(Ⅰ)设数列{an}的公比为q,数列{bn}的公差为d,由题意,q>0,
由已知有$\left\{\begin{array}{l}{2{q}^{2}-3d=2}\\{{q}^{4}-3d=10}\end{array}\right.$,消去d整理得:q4-2q2-8=0.
∵q>0,解得q=2,∴d=2,
∴数列{an}的通项公式为${a}_{n}={2}^{n-1}$,n∈N*;
数列{bn}的通项公式为bn=2n-1,n∈N*.
(Ⅱ)由(Ⅰ)有${c}_{n}=(2n-1)•{2}^{n-1}$,
设{cn}的前n项和为Sn,则
${S}_{n}=1×{2}^{0}+3×{2}^{1}+5×{2}^{2}+…+(2n-3)×{2}^{n-2}+(2n-1)×{2}^{n-1}$,
$2{S}_{n}=1×{2}^{1}+3×{2}^{2}+5×{2}^{3}+…+(2n-3)×{2}^{n-1}+(2n-1)×{2}^{n}$,
两式作差得:$-{S}_{n}=1+{2}^{2}+{2}^{3}+…+{2}^{n}-(2n-1)×{2}^{n}$=2n+1-3-(2n-1)×2n=-(2n-3)×2n-3.
∴${S}_{n}=(2n-3)•{2}^{n}+3,n∈{N}^{*}$.
点评 本题主要考查等差数列、等比数列及其前n项和,考查数列求和的基本方法和运算求解能力,是中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
20.若集合M={x|-2≤x<2},N={0,1,2},则M∩N=( )
| A. | {0} | B. | {1} | C. | {0,1,2} | D. | {0,1} |
18.阅读如图所示的程序框图,运行相应的程序,则输出i的值为( )
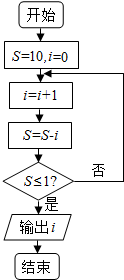

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
15.设α,β是两个不同的平面,l,m是两条不同的直线,且l?α,m?β,( )
| A. | 若l⊥β,则α⊥β | B. | 若α⊥β,则l⊥m | C. | 若l∥β,则α∥β | D. | 若α∥β,则l∥m |
9.已知A,B分别为椭圆$\frac{x{\;}^{2}}{a{\;}^{2}}$+$\frac{y{\;}^{2}}{b{\;}^{2}}$=1(a>b>0)的右顶点和上顶点,直线y=kx(k>0)与椭圆交于C,D两点,若四边形ABCD的面积最大值为2c2,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |