题目内容
14.设集合A={a2+2015|a∈N},B={b2+15|b∈N},则A∩B中的元素个数为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 A∩B中的元素个数,就是两个集合中元素相同的解的个数,列出等式关系,利用平方差化简,推出结果.
解答 解:由a2+2015=b2+15,得,b2-a2=(b+a)(b-a)=2000=24×53.因为
2000=1×2000=2×1000=4×500=5×400=8×250=10×200
=16×125=20×100=25×80=40×50
又b>a且b+a与b-a同奇偶,
所以只有
2×1000=4×500=8×250=10×200=20×100=40×50
六组有正整数解.
故选:A.
点评 本题考查集合的应用方程的解的讨论,考查集合、函数与方程的思想.

练习册系列答案
相关题目
3.双曲线$\frac{{x}^{2}}{8-k}$+$\frac{{y}^{2}}{4-k}$=1的焦点坐标是( )
| A. | (0,±$\sqrt{12-2k}$) | B. | (±$\sqrt{12-2k}$,0) | C. | (0,±2) | D. | (±2,0) |
4.下列说法中不正确的是( )
| A. | “所有金属都能导电,铁是金属,所以铁能导电”这种推理属于演绎推理 | |
| B. | 已知数据x1,x2,…,xn的方差是4,则数据-3x1+2015,-3x2+2015,…,-3xn+2015的标准差是6 | |
| C. | 用相关指数R2来刻画回归效果,R2的值越小,说明模型的拟合效果越好 | |
| D. | 若变量y和x之间的相关系数r=-0.9362,则变量y和x之间具有很强的线性相关关系 |
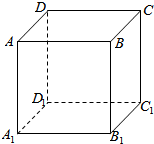 如图所示,在正方形ABCD-A1B1C1D1中:
如图所示,在正方形ABCD-A1B1C1D1中: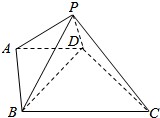 直角梯形ABCD中,∠ABC=90°,AB=AD=AP=1,BC=2,平面ABP垂直于底面ABCD.
直角梯形ABCD中,∠ABC=90°,AB=AD=AP=1,BC=2,平面ABP垂直于底面ABCD.