题目内容
(1)设不等式2x-1>m(x2-1)对满足|m|≤2的一切实数m的取值都成立,求x的取值范围;
(2)是否存在m使得不等式2x-1>m(x2-1)对满足|x|≤2的一切实数x的取值都成立.
(1)![]() (2)没有m满足题意
(2)没有m满足题意
解析:
(1)解:令f(m)=2x-1-m(x2-1)=(1-x2)m+2x-1,
可看成是一条直线,且使|m|≤2的一切
实数都有2x-1>m(x2-1)成立。
所以,![]() ,即
,即![]() ,即
,即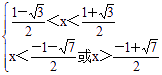
所以,![]() 。
。
(2) 令f(x)= 2x-1-m(x2-1)= -mx2+2x+(m-1),使|x|≤2的一切实数都有2x-1>m(x2-1)成立。
当![]() 时,f(x)= 2x-1在
时,f(x)= 2x-1在![]() 时,f(x)
时,f(x)![]() 。(不满足题意)
。(不满足题意)
当![]() 时,f(x)只需满足下式:
时,f(x)只需满足下式:
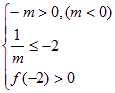 或
或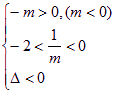 或
或
解之得结果为空集。
故没有m满足题意。

练习册系列答案
相关题目