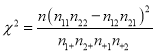题目内容
【题目】(12分) 在△ABC中,a、b、c分别为角A、B、C的对边,且![]() ,
,
(1)求![]() 的度数;
的度数;
(2)若![]() ,
, ![]() ,求b和c的值.
,求b和c的值.
【答案】解:(1)由题设得2[1-cos(B+C)]-(2cos2A-1)=![]() ,
,
∵ cos(B+C)=-cosA,∴ 2(1+cosA)-2cos2A+1=![]() ,
,
整理得(2cosA-1)2=0,∴ cosA=![]() ,∴ A=60°.
,∴ A=60°.
(2)∵ cosA=![]() =
=![]() =
=![]() =
=![]()
∴![]() =
=![]() ,∴ bc=2. 又∵ b+c=3,∴ b=1, c=2或b=2, c=1.
,∴ bc=2. 又∵ b+c=3,∴ b=1, c=2或b=2, c=1.
【解析】试题分析:本试题主要是考查了解三角形中边角的转化,以及余弦定理的运用.(1)将已知的条件![]() ,利用倍角进行降幂,得到关于角
,利用倍角进行降幂,得到关于角![]() 的三角方程,从中求解方程即可;(2)由余弦定理得
的三角方程,从中求解方程即可;(2)由余弦定理得![]() ,将
,将![]() 代入,化简得
代入,化简得![]() ,最后联立方程
,最后联立方程![]() ,求解方程即可得到
,求解方程即可得到![]() 的值.
的值.
试题解析:(1)由条件![]() 得
得![]()
∴![]() 即
即![]() ,也就是
,也就是![]()
∴![]() ,∵
,∵![]() ,∴
,∴![]()
(2)由余弦定理得, ![]() 即
即![]() ,也就是
,也就是![]()
所以![]() ,又因为
,又因为![]() ,所以
,所以![]()
联立方程![]() ,解得
,解得![]() 或
或![]() .
.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
【题目】某中学举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本,对高一年级的100名学生的成绩进行统计,并按![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组,得到成绩分布的频率分布直方图(如图)。
分组,得到成绩分布的频率分布直方图(如图)。

(1)若规定60分以上(包括60分)为合格,计算高一年级这次竞赛的合格率;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此,估计高一年级这次知识竞赛的学生的平均成绩;
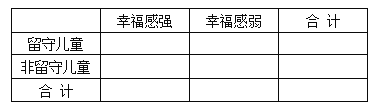
(3)若高二年级这次竞赛的合格率为![]() ,由以上统计数据填写下面
,由以上统计数据填写下面![]() 列联表,并问是否有
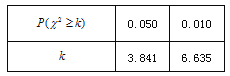
列联表,并问是否有![]() 的把握认为“这次知识竞赛的成绩与年级有关”。
的把握认为“这次知识竞赛的成绩与年级有关”。
高一 | 高二 | 合计 | |
合格人数 | |||
不合格人数 | |||
合计 |
 附:参考数据与公式
附:参考数据与公式
高一 | 合计 | ||
合格人数 | a | b | a+b |
不合格人数 | c | d | c+d |
合计 | a+c | b+d | n |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |