题目内容
已知椭圆C: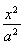 +
+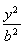 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为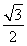 .双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
.双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
(A) 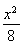 +
+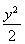 =1 (B)
=1 (B) 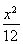 +
+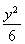 =1
=1
(C) 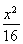 +
+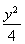 =1 (D)
=1 (D) 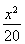 +
+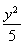 =1
=1
【答案】
D
【解析】利用椭圆离心率的概念和双曲线渐近线求法求解.
∵椭圆的离心率为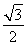 ,
,
∴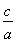 =
=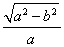 =
=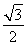 ,
,
∴a=2b.
∴椭圆方程为x2+4y2=4b2.
∵双曲线x2-y2=1的渐近线方程为x±y=0,
∴渐近线x±y=0与椭圆x2+4y2=4b2在第一象限的交点为 ,
,
∴由圆锥曲线的对称性得四边形在第一象限部分的面积为
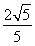 b×
b×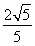 b=4,
b=4,
∴b2=5,
∴a2=4b2=20.
∴椭圆C的方程为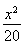 +
+ =1.
=1.
故选D.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
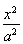



 +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,且椭圆经过点N(2,-3).
,且椭圆经过点N(2,-3).