题目内容
(本小题满分12分)如图,正方体ABCD—A1B1C1D1中,P、M、N分别为棱DD1、AB、BC的中点 .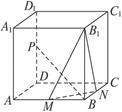
(1)求二面角B1MNB的正切值;
(2)求证:PB⊥平面MNB1;
(3)若正方体的棱长为1,画出一个正方体表面展开图,使其满足“有4个正方形面相连成一个长方形”的条件,并求出展开图中P、B两点间的距离 .
(1)解:连结BD交MN于F,连结B1F.
∵平面DD1B1B⊥平面ABCD,交线为BD,AC⊥BD,
∴AC⊥平面DD1B1B.又∵AC//MN,
∴MN⊥平面DD1B1B.
∵B1F,BF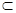 平面DD1B1B,
平面DD1B1B,
∴B1F⊥MN,BF⊥MN.
∵B1F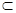 平面B1MN,
平面B1MN,
BF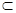 平面BMN,则∠B1FB为二面角B1-MN-B的平面角. -----------------------2分
平面BMN,则∠B1FB为二面角B1-MN-B的平面角. -----------------------2分
在Rt△B1FB中,设B1B=1,则FB=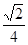 ,
,
∴tan∠B1FB=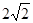 . -------------------------4分
. -------------------------4分
(2)证明:过点P作PE⊥AA1,则PE∥DA,连结BE.
又DA⊥平面ABB1A1,∴PE⊥平面ABB1A1,即PE⊥B1M.
又BE⊥B1M,∴B1M⊥平面PEB.
∴PB⊥MB1.
由(1)中MN⊥平面DD1B1B,得PB⊥MN,所以PB⊥平面MNB1. -----------------8分
(3)解:PB=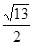 ,符合条件的正方体表面展开图可以是以下6种之一:
,符合条件的正方体表面展开图可以是以下6种之一: -------------12分
-------------12分
解析试题分析:(1)要求二面角B1-MN-B的正切值,我们要先找出二面角的平面角,再构造三角形,解三角形求出其正切值.
(2)要证明PB⊥平面B1MN,我们要在平面内找到两条与PB垂直的相交直线,分析题意可知B1M,B1N满足要求,进而可以转化为证明线线垂直.
(3)利用侧面展开图来得到BP的长度的求解。
考点:本题主要是考查二面角的平面角的求解以及线面垂直的证明问题 。
点评:解决该试题的关键是线线垂直可由线面垂直的性质推得,直线和平面垂直,这条直线就垂直于平面内所有直线,这是寻找线线垂直的重要依据.垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.本题也可以用空间向量来解决,其步骤是:建立空间直角坐系⇒明确相关点的坐标⇒明确相关向量的坐标⇒通过空间向量的坐标运算求解。

直线2x-my+1-3m=0,当m变化时,所有直线都过定点( )
A.(- ,3) ,3) | B.( ,3) ,3) |
C.( ,-3) ,-3) | D.(- ,-3) ,-3) |
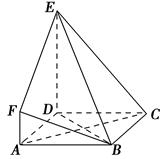
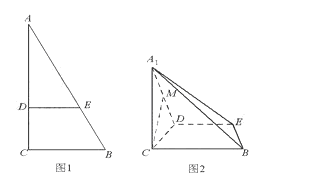
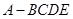 中,
中,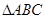 是正三角形,四边形
是正三角形,四边形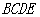 是矩形,且平面
是矩形,且平面 平面
平面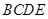 ,
,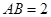 ,
,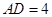 .
.
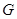 是
是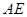 的中点,求证:
的中点,求证: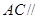 平面
平面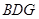 ;
;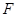 为线段
为线段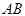 的中点,求二面角
的中点,求二面角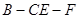 的正切值.
的正切值.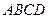 是边长为
是边长为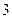 的正方形,
的正方形,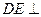 平面
平面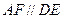 ,
, ,
, 与平面
与平面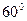

 点
点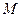 是线段
是线段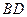 上一个动点,试确定点
上一个动点,试确定点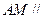 平面
平面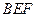 ,并证明你的结论 ;
,并证明你的结论 ; 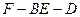 的余弦值
的余弦值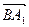 ,
,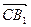 )的值;
)的值;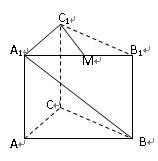
 分l2分)(注意:在试题卷上作答无效)
分l2分)(注意:在试题卷上作答无效)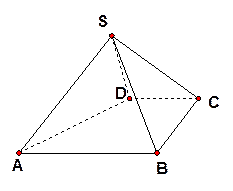
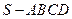 中,
中, 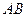 ∥
∥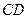 ,
,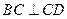 ,侧面
,侧面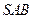 为等边三角形.
为等边三角形.
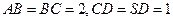 .
. 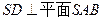
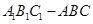 中,
中,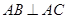 ,
,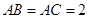 ,
,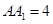 ,点
,点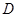 是
是 的中点.
的中点.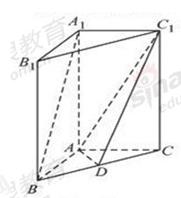
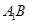 与
与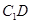 所成角的余弦值;
所成角的余弦值;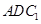 与平面
与平面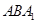 所成二面角的正弦值.
所成二面角的正弦值.