题目内容
若斜率为k的两条平行直线l,m经过曲线C的端点或与曲线C相切,且曲线C上的所有点都在l,m之间(也可在直线l,m上),则把l,m间的距离称为曲线C在“k方向上的宽度”,记为d(k).
(1)若曲线C:y=2x2-1(-1≤x≤2),求d(-1);
(2)已知k>2,若曲线C:y=x3-x(-1≤x≤2),求关于k的函数关系式d(k).
(1)若曲线C:y=2x2-1(-1≤x≤2),求d(-1);
(2)已知k>2,若曲线C:y=x3-x(-1≤x≤2),求关于k的函数关系式d(k).
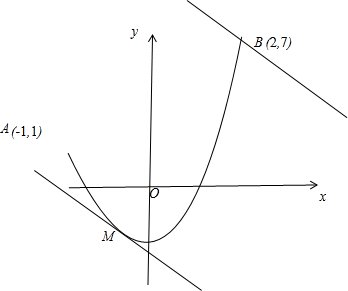
分析:(1)y=2x2-1(-1≤x≤2)的端点A(-1,1),B(2,7),对函数求导可得y′=4x,设切点M(x0,2x02-1),结合导数可判断当k=-1时,与曲线C相切的直线只有一条,另一条直线过曲线的端点B(2,7),写出两直线方程,利用两平行线的距离公式可求d(-1)
(2)曲线C:y=x3-x(-1≤x≤2)的端点C(-1,0),D(2,6),设切点N(a,a3-a),由y′=3x2-1可得k=3a2-1>2时,可得a>1或a<-1,且a2=
,则可得两平行线中的一个与直线相切与N,且切点x>1,另一条直线过A(-1,0),写出直线方程,可求
(2)曲线C:y=x3-x(-1≤x≤2)的端点C(-1,0),D(2,6),设切点N(a,a3-a),由y′=3x2-1可得k=3a2-1>2时,可得a>1或a<-1,且a2=
| 1+k |
| 3 |
解答:解:(1)∵y=2x2-1(-1≤x≤2)的端点A(-1,1),B(2,7)
∵y′=4x,设切点M(x0,2x02-1)
∴4x0=-1即x0=-
,切点M(-
,-
),
∴当k=-1时,与曲线C相切的直线只有一条,
结合题意可得,两条平行直线中一条与曲线曲线C:y=2x2-1(-1≤x≤2)相切,另一条直线过曲线的端点B(2,7)
∴平行的两条直线分别为y-7=-(x-2),y+
=-(x+
)
即x+y-9=0,x+y+
=0
由两条平行线间的距离公式可得,d=
=
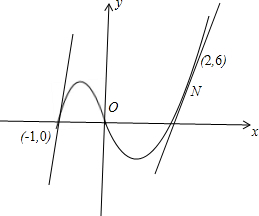
(2)曲线C:y=x3-x(-1≤x≤2)的端点C(-1,0),D(2,6),设切点N(a,a3-a)
∴y′=3x2-1
∴k=3a2-1>2时,可得a>1或a<-1,且a2=
∵-1≤a≤2∴1<a<2,即两平行线中的一个与直线相切与N,且切点x>1,另一条直线过A(-1,0)
此时两直线方程y=k(x+1),切线方程y-(a3-a)=k(x-a)
即kx-y+k=0,kx-y+a3-(k+1)a=0
两平行线间的距离d(k)=
=
∵y′=4x,设切点M(x0,2x02-1)
∴4x0=-1即x0=-
| 1 |
| 4 |
| 1 |
| 4 |
| 7 |
| 8 |
∴当k=-1时,与曲线C相切的直线只有一条,
结合题意可得,两条平行直线中一条与曲线曲线C:y=2x2-1(-1≤x≤2)相切,另一条直线过曲线的端点B(2,7)
∴平行的两条直线分别为y-7=-(x-2),y+
| 7 |
| 8 |
| 1 |
| 4 |
即x+y-9=0,x+y+
| 9 |
| 8 |
由两条平行线间的距离公式可得,d=
|
| ||
|
81
| ||
| 16 |

(2)曲线C:y=x3-x(-1≤x≤2)的端点C(-1,0),D(2,6),设切点N(a,a3-a)
∴y′=3x2-1
∴k=3a2-1>2时,可得a>1或a<-1,且a2=
| 1+k |
| 3 |
∵-1≤a≤2∴1<a<2,即两平行线中的一个与直线相切与N,且切点x>1,另一条直线过A(-1,0)
此时两直线方程y=k(x+1),切线方程y-(a3-a)=k(x-a)
即kx-y+k=0,kx-y+a3-(k+1)a=0
两平行线间的距离d(k)=
| |k-a3+(k+1)a| | ||
|
k+
| ||||||
|

点评:本题以新定义为载体,主要考查了直线与曲线的位置关系的判断,函数的导数的几何意义的应用,两点间距离公式的灵活应用是解答本题的关键

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目