题目内容
(本题满分12分)已知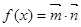 ,其中
,其中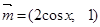 ,
,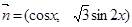
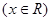 .
.
(1)求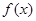 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)在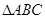 中,
中,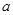 、
、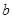 、
、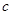 分别是角
分别是角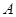 、
、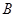 、
、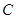 的对边,若
的对边,若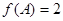 ,
,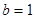 ,
,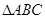 面积为
面积为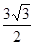 ,求:边
,求:边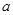 的长及
的长及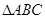 的外接圆半径
的外接圆半径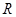 .
.
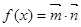 ,其中
,其中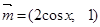 ,
,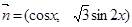
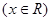 .
.(1)求
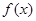 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;(2)在
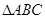 中,
中,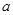 、
、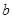 、
、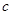 分别是角
分别是角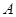 、
、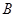 、
、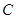 的对边,若
的对边,若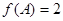 ,
,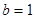 ,
,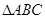 面积为
面积为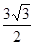 ,求:边
,求:边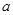 的长及
的长及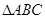 的外接圆半径
的外接圆半径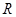 .
.(1)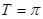 ;单调递增区间
;单调递增区间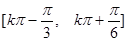
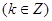 .
.
(2)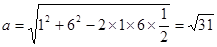 ;
;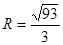 .
.
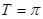 ;单调递增区间
;单调递增区间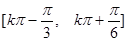
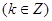 .
.(2)
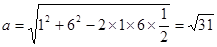 ;
;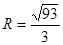 .
.:(1)由平面向量的数量积公式和三角函数的公式把函数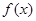 化简,利用正弦函数的周期性和单调性求得周期和单调增区间;
化简,利用正弦函数的周期性和单调性求得周期和单调增区间;
(2)结合(1)可求得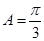 ,由三角形的面积公式得
,由三角形的面积公式得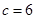 ,由余弦定理得
,由余弦定理得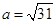 ,根据正弦定理的变形得
,根据正弦定理的变形得
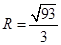 。
。
解 :(1)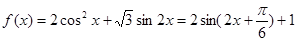 …………2分
…………2分
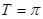 ………………3分
………………3分
单调递增区间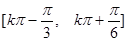
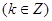 ……………4分
……………4分
(2)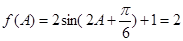 ,由
,由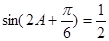 ,得
,得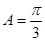 …………6分
…………6分
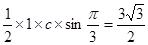 ,
,
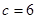 …………8分
…………8分
 …………10分
…………10分
 ,
,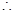
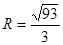 …………12分
…………12分
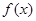 化简,利用正弦函数的周期性和单调性求得周期和单调增区间;
化简,利用正弦函数的周期性和单调性求得周期和单调增区间;(2)结合(1)可求得
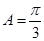 ,由三角形的面积公式得
,由三角形的面积公式得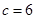 ,由余弦定理得
,由余弦定理得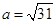 ,根据正弦定理的变形得
,根据正弦定理的变形得
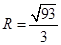 。
。解 :(1)
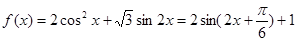 …………2分
…………2分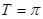 ………………3分
………………3分单调递增区间
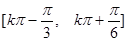
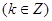 ……………4分
……………4分(2)
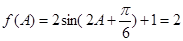 ,由
,由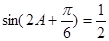 ,得
,得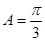 …………6分
…………6分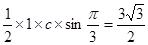 ,
,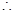
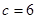 …………8分
…………8分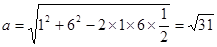 …………10分
…………10分 ,
,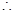
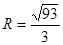 …………12分
…………12分
练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
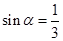 ,
,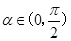 ,
,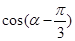 的值;(2)求
的值;(2)求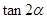 的值.
的值.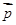 =(
=(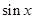 ,
,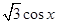 ),
),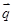 =(
=(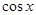 ,
,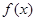 =
=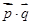
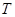 ;
; 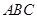 的三边长
的三边长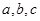 成等比数列,且
成等比数列,且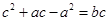 ,求边
,求边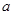 所对角
所对角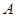 以及
以及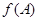 的大小。
的大小。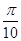 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是( )
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是( )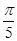 )
)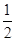 x-
x- )
) ,函数
,函数 的定义域为
的定义域为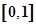 且
且 ,
, 当
当 时有
时有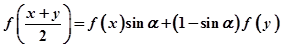
 ;
; 的值;
的值; 的单调增区间.
的单调增区间.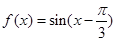 的一个单调增区间是( )
的一个单调增区间是( ) )
) )
) )
) )
) 角的直路
角的直路 ,交点为
,交点为 ,甲、乙分别在
,甲、乙分别在 上,起初甲离
上,起初甲离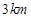 ,乙离
,乙离 ,后来甲沿
,后来甲沿 的方向,乙沿
的方向,乙沿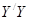 的方向,同时以
的方向,同时以 的速度步行。
的速度步行。 小时后两人的距离是多少?
小时后两人的距离是多少?
 ,且
,且 ,则
,则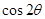 的值为( )
的值为( )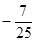



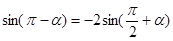 ,则
,则