题目内容
如图,有两条相交成 角的直路
角的直路 ,交点为
,交点为 ,甲、乙分别在
,甲、乙分别在 上,起初甲离
上,起初甲离 点
点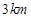 ,乙离
,乙离 点
点 ,后来甲沿
,后来甲沿 的方向,乙沿
的方向,乙沿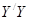 的方向,同时以
的方向,同时以 的速度步行。
的速度步行。
(1)起初两人的距离是多少?
(2) 小时后两人的距离是多少?
小时后两人的距离是多少?
(3)什么时候两人的距离最短,并求出最短距离。
 角的直路
角的直路 ,交点为
,交点为 ,甲、乙分别在
,甲、乙分别在 上,起初甲离
上,起初甲离 点
点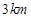 ,乙离
,乙离 点
点 ,后来甲沿
,后来甲沿 的方向,乙沿
的方向,乙沿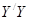 的方向,同时以
的方向,同时以 的速度步行。
的速度步行。(1)起初两人的距离是多少?
(2)
 小时后两人的距离是多少?
小时后两人的距离是多少?(3)什么时候两人的距离最短,并求出最短距离。

(1)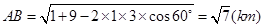 (2)
(2) 小时后,甲乙两人的距离为
小时后,甲乙两人的距离为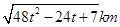 (3)
(3)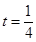 时两人的距离最短,最短距离为
时两人的距离最短,最短距离为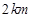
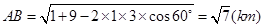 (2)
(2) 小时后,甲乙两人的距离为
小时后,甲乙两人的距离为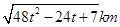 (3)
(3)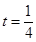 时两人的距离最短,最短距离为
时两人的距离最短,最短距离为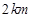
连接AB构成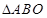 ,再用由余弦定理写出AB(CD)的表达式,
,再用由余弦定理写出AB(CD)的表达式,
(2)中由于甲先到达O点,所以分类讨论,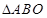 还是
还是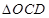 ;
;
(3)将二次函数表达式化成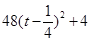 ,求解就容易了。
,求解就容易了。
解:设甲、乙两人起初所在位置分别为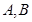 ,连接
,连接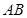 。
。
(1)在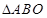 中,由余弦定理,得
中,由余弦定理,得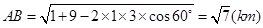 ……3分
……3分
(2)设 小时后,甲由
小时后,甲由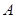 运动到
运动到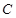 ,乙由
,乙由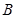 运动到
运动到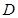 ,连接
,连接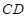
当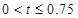 时,
时,
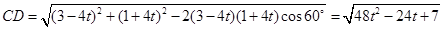 ……7分
……7分
当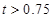 时,在
时,在 中,
中,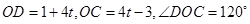
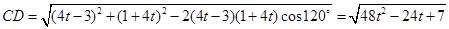 ……11分
……11分
∴ 小时后,甲乙两人的距离为
小时后,甲乙两人的距离为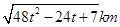 ……12分
……12分
(3)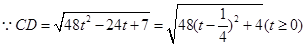
∴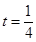 时两人的距离最短,最短距离为
时两人的距离最短,最短距离为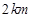
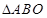 ,再用由余弦定理写出AB(CD)的表达式,
,再用由余弦定理写出AB(CD)的表达式,(2)中由于甲先到达O点,所以分类讨论,
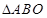 还是
还是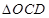 ;
;(3)将二次函数表达式化成
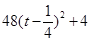 ,求解就容易了。
,求解就容易了。解:设甲、乙两人起初所在位置分别为
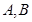 ,连接
,连接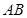 。
。(1)在
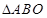 中,由余弦定理,得
中,由余弦定理,得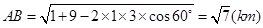 ……3分
……3分(2)设
 小时后,甲由
小时后,甲由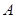 运动到
运动到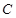 ,乙由
,乙由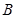 运动到
运动到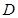 ,连接
,连接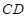
当
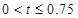 时,
时,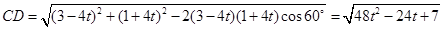 ……7分
……7分当
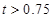 时,在
时,在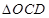 中,
中,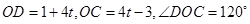
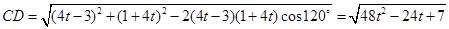 ……11分
……11分∴
 小时后,甲乙两人的距离为
小时后,甲乙两人的距离为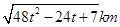 ……12分
……12分(3)
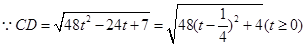
∴
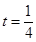 时两人的距离最短,最短距离为
时两人的距离最短,最短距离为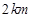

练习册系列答案
相关题目
 的图象向右平移
的图象向右平移 个单位得到的函数解析式为( )
个单位得到的函数解析式为( )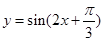
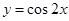

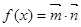 ,其中
,其中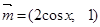 ,
,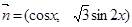
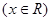 .
.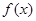 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;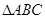 中,
中,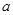 、
、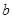 、
、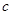 分别是角
分别是角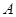 、
、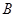 、
、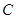 的对边,若
的对边,若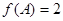 ,
,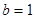 ,
,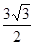 ,求:边
,求:边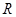 .
.
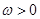 ,函数
,函数 的图像向右平移
的图像向右平移 个单位后与原图像重合,则
个单位后与原图像重合,则 的最小值为 .
的最小值为 .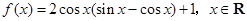 .
.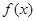 的单调递增取区间;
的单调递增取区间;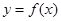 的图象向左平移
的图象向左平移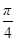 个单位后,再将图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数
个单位后,再将图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数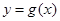 的图象,求
的图象,求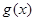 的最大值及取得最大值时的
的最大值及取得最大值时的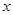 的集合.
的集合. ,求
,求 时,求函数的值域
时,求函数的值域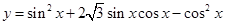 ,
,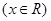 (13分)
(13分) 时,求函数的值域。
时,求函数的值域。 (其中
(其中 ,
, ).若点
).若点 在函数
在函数 的图像上,则
的图像上,则 的值为
的值为