题目内容
(本题满分14分)
已知向量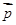 =(
=(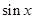 ,
,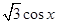 ),
),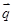 =(
=(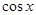 ,
,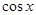 ),定义函数
),定义函数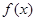 =
=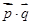
(1)求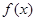 的最小正周期
的最小正周期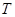 ;
;
(2)若△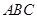 的三边长
的三边长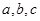 成等比数列,且
成等比数列,且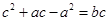 ,求边
,求边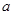 所对角
所对角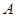 以及
以及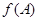 的大小。
的大小。
已知向量
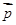 =(
=(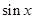 ,
,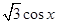 ),
),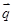 =(
=(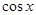 ,
,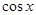 ),定义函数
),定义函数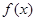 =
=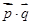
(1)求
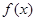 的最小正周期
的最小正周期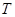 ;
; (2)若△
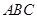 的三边长
的三边长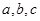 成等比数列,且
成等比数列,且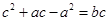 ,求边
,求边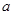 所对角
所对角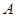 以及
以及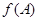 的大小。
的大小。 (1) T=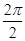 =π.(2) A=
=π.(2) A=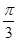 .f(A)==
.f(A)== .
.
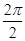 =π.(2) A=
=π.(2) A=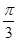 .f(A)==
.f(A)== .
.本试题主要考查了三角函数的化简以及性质的运用。第一问中首先
p·q=(sin x,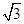 cos x)·(cos x,cos x)=sin xcos x+
cos x)·(cos x,cos x)=sin xcos x+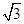 cos2x
cos2x
= sin 2x+
sin 2x+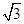 ·
·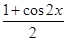 =
= sin 2x+
sin 2x+ cos 2x+
cos 2x+
=sin(2x+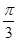 )+
)+ .
.
利用周期公式,得到结论。
第二问中,∵a、b、c成等比数列,∴b2=ac,
又c2+ac-a2=bc.
∴cos A= =
=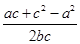 =
=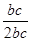 =
=
f(A)=sin(2×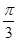 +
+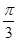 )+
)+ =sin π+
=sin π+ =
= .
.
解:(1)f(x)=
p·q=(sin x,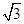 cos x)·(cos x,cos x)=sin xcos x+
cos x)·(cos x,cos x)=sin xcos x+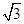 cos2x…………2分
cos2x…………2分
= sin 2x+
sin 2x+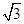 ·
·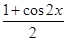 =
= sin 2x+
sin 2x+ cos 2x+
cos 2x+
=sin(2x+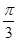 )+
)+ .………………………………4分
.………………………………4分
∴f(x)的最小正周期为T=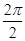 =π.……………………………6分
=π.……………………………6分
(2)∵a、b、c成等比数列,∴b2=ac,…………………………7分
又c2+ac-a2=bc.
∴cos A= =
=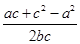 =
=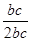 =
= .……………………10分
.……………………10分
又∵0<A<π,∴A=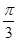 .……………………………………12分
.……………………………………12分
f(A)=sin(2×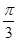 +
+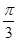 )+
)+ =sin π+
=sin π+ =
= .……………………14分
.……………………14分
p·q=(sin x,
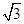 cos x)·(cos x,cos x)=sin xcos x+
cos x)·(cos x,cos x)=sin xcos x+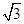 cos2x
cos2x =
 sin 2x+
sin 2x+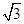 ·
·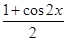 =
= sin 2x+
sin 2x+ cos 2x+
cos 2x+
=sin(2x+
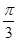 )+
)+ .
.利用周期公式,得到结论。
第二问中,∵a、b、c成等比数列,∴b2=ac,
又c2+ac-a2=bc.
∴cos A=
 =
=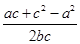 =
=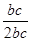 =
=
f(A)=sin(2×
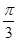 +
+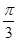 )+
)+ =sin π+
=sin π+ =
= .
.解:(1)f(x)=
p·q=(sin x,
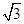 cos x)·(cos x,cos x)=sin xcos x+
cos x)·(cos x,cos x)=sin xcos x+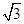 cos2x…………2分
cos2x…………2分=
 sin 2x+
sin 2x+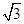 ·
·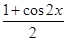 =
= sin 2x+
sin 2x+ cos 2x+
cos 2x+
=sin(2x+
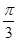 )+
)+ .………………………………4分
.………………………………4分∴f(x)的最小正周期为T=
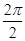 =π.……………………………6分
=π.……………………………6分(2)∵a、b、c成等比数列,∴b2=ac,…………………………7分
又c2+ac-a2=bc.
∴cos A=
 =
=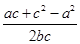 =
=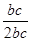 =
= .……………………10分
.……………………10分又∵0<A<π,∴A=
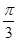 .……………………………………12分
.……………………………………12分f(A)=sin(2×
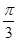 +
+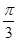 )+
)+ =sin π+
=sin π+ =
= .……………………14分
.……………………14分
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
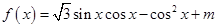
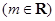 的图象过点
的图象过点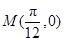 .
.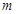 的值;
的值; 中,角
中,角 ,
, ,
, 的对边分别是
的对边分别是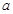 ,
,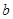 ,
,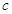 .若
.若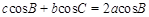 ,求
,求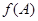 的取值范围.
的取值范围.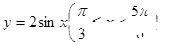 的值域是
的值域是 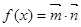 ,其中
,其中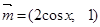 ,
,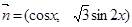
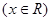 .
.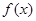 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;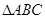 中,
中,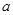 、
、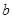 、
、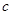 分别是角
分别是角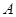 、
、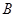 、
、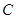 的对边,若
的对边,若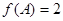 ,
,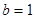 ,
,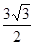 ,求:边
,求:边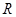 .
.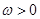 ,函数
,函数 的图像向右平移
的图像向右平移 个单位后与原图像重合,则
个单位后与原图像重合,则 的最小值为 .
的最小值为 .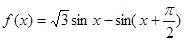 的单调递增区间__________________.
的单调递增区间__________________.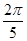 ,半径等于20,则扇形的面积为( )
,半径等于20,则扇形的面积为( )
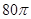
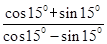 =_________
=_________  ,则
,则 ( )
( )


