题目内容
【题目】已知函数 
，若m＜n，且f（m）=f（n），则n﹣m的取值范围是（ ）
A.[3﹣2ln2，2）
B.[3﹣2ln2，2]
C.[e﹣1，2]
D.[e﹣1，2）
【答案】A
【解析】解：作出函数f（x）的图象如图：
若m＜n，且f（m）=f（n），
则当ln（x+1）=1时，得x+1=e，即x=e﹣1，
则满足0＜n≤e﹣1，﹣2＜m≤0，
则ln（n+1）= 
m+1，即m=2ln（n+1）﹣2，
则n﹣m=n+2﹣2ln（n+1），
设h（n）=n+2﹣2ln（n+1），0＜n≤e﹣1
则h′（n）=1﹣ 
= 
= 
，
当h′（x）＞0得1＜n≤e﹣1，
当h′（x）＜0得0＜n＜1，
即当n=1时，函数h（n）取得最小值h（1）=1+2﹣2ln2=3﹣2ln2，
当n=0时，h（0）=2﹣2ln1=2，
当n=e﹣1时，h（e﹣1）=e﹣1+2﹣2ln（e﹣1+1）=1+e﹣2=e﹣1＜2，
则3﹣2ln2≤h（n）＜2，
即n﹣m的取值范围是[3﹣2ln2，2），
故选：A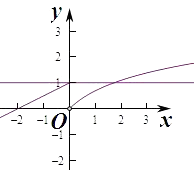
练习册系列答案
相关题目
【题目】某便利店计划每天购进某品牌鲜奶若干件，便利店每销售一瓶鲜奶可获利
元；若供大于求，剩余鲜奶全部退回，但每瓶鲜奶亏损
元；若供不应求，则便利店可从外调剂，此时每瓶调剂品可获利
元.
（1）若便利店一天购进鲜奶
瓶，求当天的利润
（单位：元）关于当天鲜奶需求量
（单位：瓶，
）的函数解析式；
（2）便利店记录了
天该鲜奶的日需求量（单位：瓶，）整理得下表：
日需求量 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
若便利店一天购进瓶该鲜奶，以天记录的各需求量的频率作为各需求量发生的概率，求当天利润在区间
内的概率.
