题目内容
有下列命题：
①设集合M={x|0＜x≤3}，N={x|0＜x≤2}，则“a∈M”是“a∈N”的充分而不必要条件；
②“|
+
|＜1”是“|
|+|
|＜1”的必要不充分条件；
③“a=1”是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件；
④命题P：“?x0∈R，x02-x0-1＞0”的否定?P：“?x∈R，x2-x-1≤0”．
则上述命题中为真命题的是（ ）
①设集合M={x|0＜x≤3}，N={x|0＜x≤2}，则“a∈M”是“a∈N”的充分而不必要条件；
②“|
| a |
| b |
| a |
| b |
③“a=1”是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件；
④命题P：“?x0∈R，x02-x0-1＞0”的否定?P：“?x∈R，x2-x-1≤0”．
则上述命题中为真命题的是（ ）
分析：①由集合M={x|0＜x≤3}?N={x|0＜x≤2}，则a∈N⇒a∈M，但a∈M时，如a∉N不一定成立，可判断①
②由|
+
|≤|
|+|
|，可判断②
③若a=1，则直线x-ay=0与直线x+ay=0互相垂直；但直线x-ay=0与x+ay=0垂直，则a2-1=0，可判断故③
④个根据特称命题命题P：“?x0∈R，x02-x0-1＞0”的否定是全称命题可判断④
②由|
| a |
| b |
| a |
| b |
③若a=1，则直线x-ay=0与直线x+ay=0互相垂直；但直线x-ay=0与x+ay=0垂直，则a2-1=0，可判断故③
④个根据特称命题命题P：“?x0∈R，x02-x0-1＞0”的否定是全称命题可判断④
解答：解：①由于集合M={x|0＜x≤3}?N={x|0＜x≤2}，则a∈N⇒a∈M，但a∈M时，如a=3∉N，从而可得“a∈M”是“a∈N”的必要而不充分条件，故①错误
②由于|
+
|≤|
|+|
|，
若|
|+|
|＜1，则|
|+|
|＜1不一定成立；若|
|+|
|＜1，则|
+
|＜1一定成立，即|
+
|＜1是|
|+|
|＜1的必要不充分条件，故②正确
③若a=1，则直线x-ay=0与直线x+ay=0互相垂直；若直线x-ay=0与x+ay=0垂直，则a2-1=0即a=±1，故③错误
④命题P：“?x0∈R，x02-x0-1＞0”的否定?P：“?x∈R，x2-x-1≤0”．故④正确
故选C
②由于|
| a |
| b |
| a |
| b |
若|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
③若a=1，则直线x-ay=0与直线x+ay=0互相垂直；若直线x-ay=0与x+ay=0垂直，则a2-1=0即a=±1，故③错误
④命题P：“?x0∈R，x02-x0-1＞0”的否定?P：“?x∈R，x2-x-1≤0”．故④正确
故选C
点评：本题主要考查了命题的真假判断，解题的关键是熟练掌握基本知识并能灵活应用，解答此类试题，对考试的知识的掌握的要求较高
练习册系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
距离的和等于定长的点的轨迹是椭圆；
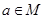，则
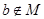”的逆否命题是：若
；
曲线
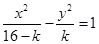表示双曲线
，则
”的逆否命题是：若
；
是假命题，则
都是假命题；
”的否定
：“
”