题目内容
有下列命题:
①设集合M={x|0<x≤3},N={x|0<x≤2},则“a∈M”是“a∈N”的充分而不必要条件;
②命题“若a∈M,则b∉M”的逆否命题是:若b∈M,则a∉M;
③若p∧q是假命题,则p,q都是假命题;
④命题P:“?x0∈R,x02-x0-1>0”的否定¬P:“?x∈R,x2-x-1≤0”
则上述命题中为真命题的有
①设集合M={x|0<x≤3},N={x|0<x≤2},则“a∈M”是“a∈N”的充分而不必要条件;
②命题“若a∈M,则b∉M”的逆否命题是:若b∈M,则a∉M;
③若p∧q是假命题,则p,q都是假命题;
④命题P:“?x0∈R,x02-x0-1>0”的否定¬P:“?x∈R,x2-x-1≤0”
则上述命题中为真命题的有
②④
②④
(填序号)分析:①由集合M={x|0<x≤3}?N={x|0<x≤2},则a∈N⇒a∈M,但a∈M时,如a∉N不一定成立,可判断①;
②根据逆否命题的定义,写出原命题“若a∈M,则b∉M”的逆否命题,可判断②;
③根据复合命题真假判断的真值表,可判断③;
④根据存在性命题的否定方法,写出原命题的否定形式,可判断④
②根据逆否命题的定义,写出原命题“若a∈M,则b∉M”的逆否命题,可判断②;
③根据复合命题真假判断的真值表,可判断③;
④根据存在性命题的否定方法,写出原命题的否定形式,可判断④
解答:解:∵集合M={x|0<x≤3},N={x|0<x≤2},
∴M?N,则a∈N⇒a∈M,但a∈M时,如a∉N不一定成立,
故“a∈M”是“a∈N”的必要不充分条件,故①为假命题;
命题“若a∈M,则b∉M”的逆否命题是:若b∈M,则a∉M,故②为真命题;
若p∧q是假命题,则p,q存在至少一个是假命题,但不一定都是假命题,故③为假命题;
命题P:“?x0∈R,x02-x0-1>0”的否定¬P:“?x∈R,x2-x-1≤0”,故④为真命题;
故答案为:②④
∴M?N,则a∈N⇒a∈M,但a∈M时,如a∉N不一定成立,
故“a∈M”是“a∈N”的必要不充分条件,故①为假命题;
命题“若a∈M,则b∉M”的逆否命题是:若b∈M,则a∉M,故②为真命题;
若p∧q是假命题,则p,q存在至少一个是假命题,但不一定都是假命题,故③为假命题;
命题P:“?x0∈R,x02-x0-1>0”的否定¬P:“?x∈R,x2-x-1≤0”,故④为真命题;
故答案为:②④
点评:本题考查的知识点是命题的真假判断与应用,复合命题的真假,四种命题,充要条件,全(特)称命题的否定,是简单逻辑的综合应用,难度不大.

练习册系列答案
相关题目
 距离的和等于定长的点的轨迹是椭圆;
距离的和等于定长的点的轨迹是椭圆;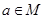 ,则
,则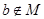 ”的逆否命题是:若
”的逆否命题是:若 ;
;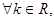 曲线
曲线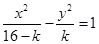 表示双曲线
表示双曲线 ,则
,则 ”的逆否命题是:若
”的逆否命题是:若 ;
; 是假命题,则
是假命题,则 都是假命题;
都是假命题; ”的否定
”的否定 :“
:“ ”
”