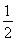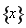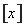题目内容
已知关于x的二次方程x2+2mx+2m+1=0.
(1)若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求实数m的取值范围;
(2)若方程两根均在区间(0,1)内,求实数m的取值范围.
(1)-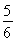 <m<-
<m<-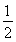 .(2)-
.(2)-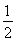 <m≤1-
<m≤1-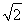
【解析】设二次方程x2+2mx+2m+1=0所对应的函数为f(x)=x2+2mx+2m+1.
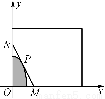
(1)要使方程的一根在区间(-1,0)内,另一根在区间(1,2)内,则结合函数图象(如图),
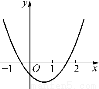
有 解得-
解得-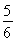 <m<-
<m<-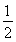 .
.
(2)要使方程两根均在区间(0,1)内,则结合函数图象(如图),
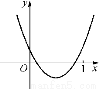
有 解得
解得 即-
即-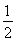 <m≤1-
<m≤1-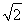

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法计算,其参考数据如下:
f(1)=-2 | f(1.5)=0.625 | f(1.25)=-0.984 |
f(1.375)=-0.260 | f(1.4375)=0.162 | f(1.40625)=-0.054 |
那么方程x3+x2-2x-2=0的一个近似根为________(精确到0.1).