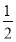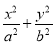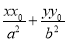Question

设命题p：f(x)＝在区间(1，＋∞)上是减函数；命题q：x1，x2是方程x2－ax－2＝0的两个实根，且不等式m2＋5m－3≥|x1－x2|对任意的实数a∈[－1,1]恒成立．若p∧q为真，试求实数m的取值范围．

 

Answer 1

(1，＋∞)

【解析】由于f(x)＝的单调递减区间是(－∞，m)和(m，＋∞)，而f(x)又在(1，＋∞)上是减函数，

所以m≤1，即p：m≤1.

对于命题q：|x1－x2|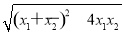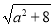＝＝≤3. ?

则m2＋5m－3≥3，即m2＋5m－6≥0，

解得m≥1或m≤－6，

若綈p∧q为真，则p假q真，

所以

解之得m＞1.

因此实数m的取值范围是(1，＋∞)．